PCA - webdancer's Blog
PCA
PCA是一种降低数据特征维度的技术。它通过将高维空间数据正交投影到低维子空间,使投影空间中数据的方差最大来实现。另外的一种理解是它通过将高维空间数据正交投影到低维子空间,最小化从投影数据恢复到原数据的误差。PCA带来的好处是数据压缩后,能有更小的存储要求,有更快的分类速度;但是带来的坏处就是,在数据压缩的过程中,可能会丢失一些特征。
1.投影
在PCA形式化表示的时候需要用到向量投影的知识,这里我们简单看一下。两个向量:$\vec{a},\vec{b}$,我们将$\vec{b}$正交投影到$\vec{a}$上,如下图所示:
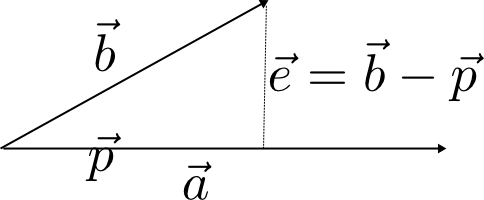
我们将投影向量表示为:$\vec{p}={\vec{a}x}$,将垂直于向量$\vec{a}$的向量$\vec{e}=\vec{b}-\vec{p}=\vec{b}-\vec{a}x$。
根据两个向量:$\vec{p},\vec{e}$的垂直关系,则可以得出:
\[
\vec{p}^{T}\vec{e}=0\\
\Rightarrow (\vec{a}x)^{T}(\vec{b}-\vec{a}x)=0\\
\Rightarrow (\vec{a}x)^{T}\vec{b} = (\vec{a}x)^{T}\vec{a}x\\
\Rightarrow \vec{a}^{T}x\vec{b} = \vec{a}^{T}x\vec{a}x\\
\Rightarrow x=\frac{\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}}
\]
通过上面的推导得出x的值,即投影向量的长度。那么投影向量:
\[
\vec{p}=\vec{a}x=\frac{\vec{a}\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}}=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}\vec{b}
\]
则如果我们右侧的矩阵定义为投影矩阵$P=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}$。另外:投影矩阵有两个性质:$P=P^{T};P=P^{2}$。这三个公式是下面我们进行向量运算的一个基础。注意:在高维情况下,推导过程基本类似,可以得出基本类似的过程,不过投影矩阵的表达形式不同,可以参考线性代数的教科书,形式为:$P=A(A^TA)^{-1}A^T$,其中,$A=(a_1,a_2,..a_n)$.
2.最大化投影数据的方差
如上图所示,我们选择不同的投影子空间,就会有不同的投影点。根据PCA的概念,我们选择一个投影子空间使得投影数据的方差最大。那么下面我们就来形式化这个过程。
我们的数据集为:N个D维的数据点,表示为:${x_1,x_2,...,x_N}$。
i.投影到1维空间的情况。
我们先来看一下最简单的情况,把D维数据投影到一维的情况,设投影的方向向量为:$u$(不失一般性,我们假设$u$为单位向量,即$u^Tu=1$),根据上面我们的投影推导可以得出投影矩阵为:$P=uu^{T}$,投影点表示为:$Px=uu^{T}x$。那么可以得出投影点向量的长度为:$u^{T}x$。那么,投影点的期望表示为:
\[
\mathbb E(\hat x)=\frac{1}{N}\sum_{n=1}^{N}u^{T}x=u^{T}\frac{1}{N}\sum_{n=1}^{N}x=u^{T}\bar{x}
\]
其中,$\bar{x}=\frac{1}{N}\sum_{n=1}^{N}x$
投影空间中数据点的方差表示为:
\[
\frac{1}{N}\sum_{n=1}^{N}\{u^{T}x-u^{T}\bar{x}\}^{2}=u^{T}Su
\]
其中:$S=\frac{1}{N}\sum_{n=1}^{N}\{x-\bar{x}\}^{2}$(上面式子再推导的过程中用到了$\|a\|^2=a^Ta$)。
这样我们就得到了目标函数:
\[
J(u)=argmax_{u}u^{T}Su \\
s.t.u^{T}u=1
\]
这样我们就得到了一个有约束的优化问题,使用Lagrange Multipler 方法,可以得到:
\[
J(u)=argmax_{u}\{u^{T}Su+\lambda_1(1-u^{T}u)\}
\]
求导,然后得到式子:$Su-\lambda_1u=0 \Rightarrow Su=\lambda_1u$,将这个式子再代入目标函数$J(u)$,得到:
\[
J(u)=argmax_{u}u^{T}Su \Rightarrow J=argmax\lambda_1 \\
s.t.u^{T}u=1
\]
这样我们就可以看到,我们目标函数的最大值就是最大的特征值,这样我们的向量$u$就是最大特征值对应的特征向量,这样就找到了我们的投影子空间。
ii.投影到M(M<D)维空间的情况。
把D维数据投影到M维的情况与投影到一维的情况大体相差不多。我在推导的过程中存在的一个主要的盲点就是:在高维的情况下,投影点的方差如何表示的问题,以及里面的矩阵变化。
设投影的方向向量为:$U=(u_1,u_2,...,u_M)$(不失一般性,我们假设$u_i$为单位向量,即$u^Tu=1$),根据上面我们的投影推导可以得出投影矩阵为:$P=UU^{T}$(我们选择的$u_i$都是单位向量,导致(U^{T}U)^{-1}是单位矩阵),投影点表示为:$Px=UU^{T}x$。过程与上面的差不多,投影空间中数据点的方差表示为:
\[
\frac{1}{N}\sum_{n=1}^{N}\{U^{T}x-U^{T}\bar x \}^{T}\{U^{T}x-U^{T}\bar x\}\\
\Rightarrow trace(\frac{1}{N}\sum_{n=1}^{N}\{U^{T}x-U^{T}\bar x\}\{U^{T}x-U^{T}\bar x^{T}\}^{T})\\
\Rightarrow trace(U^{T}\frac{1}{N}\sum_{n=1}^{N}\{x-\bar x\}\{x-\bar x\}^{T}U)\\
\Rightarrow trace(U^{T}SU)
\]
其中:$S=\frac{1}{N}\sum_{n=1}^{N}\{x-\bar x\}\{x-\bar x\}^{T}; \bar{x}=\frac{1}{N}\sum_{n=1}^{N}x$
这样我们就得到了目标函数:
J(U)=argmax_{U}trace(U^{T}SU)=argmax_{U}\sum_{m=1}^{M}u_m^{T}\\
s.t. U^{T}U=I
\]
这样我们就得到了一个有约束的优化问题,使用Lagrange Multipler 方法,可以得到:
\[
J(U)=argmax_{U}argmax_{U}\sum_{m=1}^{M}u_m^{T}Su_m+\sum_{m=1}^{M}\lambda_m(1-u_m^Tu_m)
\]
对$u_m$求偏导,然后得到式子:$Su_m-\lambda_mu_m=0 \Rightarrow Su_m=\lambda_mu_m$,将这个式子再代入目标函数$J(u)$,得到:
J(U)=argmax_{U}trace(U^{T}SU)=argmax_{U}\sum_{m=1}^{M}u_m^{T}Su_m\\
\Rightarrow J=argmax\sum_{m=1}^M\lambda_m\\
s.t. U^{T}U=I
\]
这样我们就可以看到,我们目标函数的最大值就是求前M个最大的特征值,这样我们的向量$u_m$就是特征值对应的特征向量,这样就找到了我们的投影子空间。
3.最小化投影误差函数
将投影点从投影空间恢复到原空间的式子为:$\hat x_i=\sum_{i=1}z_{ni}u_i+b$,则我们很容易写出误差函数(欧式距离):
\[
J(z,u,b)=argmin_(z,u,b)\frac{1}{N}\sum_{n=1}^{N}\|x_n-\hat x_i\|^2 \\
s.t. U^{T}U=I
\]
对上面的式子分别对$z,b$求偏导数,可以得出:
$z_{ni}^*=x_n^Tu_i,b^*=\bar x$(这里用到的一个小trick还是$\|a\|^2=a^Ta$,展开后求解偏导数会容易很多)
然后将上面求出来的代入目标函数,可以得到关于u的函数,
\[
J(z*,u,b*)=argmin_u\frac{1}{N}\sum_{n=1}{N}\|x_n-\hat x_i\|^2 代入即可)\\
\Rightarrow J(U)=argmax_{U}trace(U^{T}SU)=argmax_{U}\sum_{m=1}^{M}u_m^{T}Su_m\\
s.t. U^{T}U=I
\]
这样我们就得到了与(2)最大化投影方差相同的目标函数。下面的过程就与上面相同了,也转到了求前M个最大特征向量。
4.方差的理解[2]
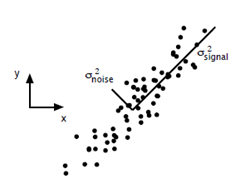
5.特征值,特征向量求解
在matlab中,可以使用eig或是svd来求解特征值。具体的求解算法这里不详细讨论了。关于SVD这里有一篇文章,记录的很详细。
6.PCA的应用
PCA的一个应用就是进行维度下降,比如在人脸识别应用中,使用PCA可以生成eighface。
如下图的10幅人脸:

经过PCA降维,得到的特征向量为(展示成图象):
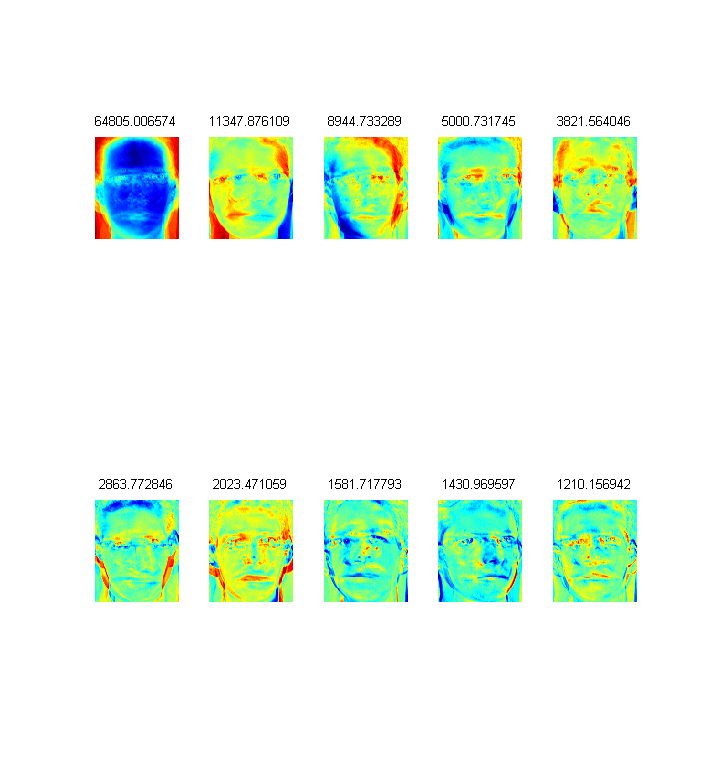
pca的另一个应用就是数据可视化。
7.总结
PCA是一种传统的统计分析方法,将高维空间数据投影到低维子空间,在这个过程中尽量保持原有数据的主要信息。但是,PCA由于没有考虑类别信息,可能会丢失类别信息。PCA算法总结如下:
1.对数据进行归一化(data normalization)
2.计算数据集合的协方差矩阵(covariance matrix computing)
3.计算(2)中求得的协方差矩阵的特征值,特征向量
4.根据投影空间维数选择投影空间基向量,计算投影点
【引用】:
1.prml

2022年12月24日 02:44
You may be asking how to delete Instagram messages because you want to clear up your inbox of spam messages. Perhaps your need to erase texts is a reflex reaction to an emotionally charged scenario. Clear Instagram Messages There are both good and negative reasons to delete your conversations and bear in mind that this is a final decision, so make it carefully. Here’s all you need to know about erasing or deleting Instagram direct messages.
2023年2月07日 21:41
BSNL is installing Bharat Net a country-wide fiber optic cable for internet connectivity in many of the panchayats, and on the other hand, ISP brought the same fibernet technology to your doorstep directly and through TIPs. FTTH BSNL Telecom Infrastructure Providers (TIPs) with new BSNL Fiber plans covering many isolated pockets in all BSNL circles of the country for 50Mbps to 300 Mbps internet speed on providing with BSNL Fiber Plans along with FREE ONT as per the possibility.