Neural Networks笔记0 - webdancer's Blog
Neural Networks笔记0
这里记录一下Neural Networks学习的内容,这里的NN指的是Artificial neural networks(人工神经网络)。
1.历史
正如每一种技术的经历一样,Neural Networks(NN)的发展过程也是曲折的。从计算机科学家试图对神经学家的神经网络用计算机建模,发明了Artificial neural networks,科学家经历了欣喜,质疑,重新发展的一个过程。20 世纪 90 年代中期之前,“从例子中学习”的另一大主流技术是基于神经网络的连接主义学习。连接主义学习技术在 20 世纪 50 年代曾经历了一个大发展时期,但因为早期的很多人工智能研究者对符号表示有特别的偏爱,例如H. Simon曾说人工智能就是研究“对智能行为的符号化建模”,因此当时连接主义的研究并没有被纳入主流人工智能的范畴。同时,连接主义学习自身也遇到了极大的问题,M. Minsky和S. Papert在 1969 年指出,(当时的)神经网络只能用于线性分类,对哪怕“异或”这么简单的问题都做不了。于是,连接主义学习在此后近 15 年的时间内陷入了停滞期。直到1983 年,J.J. Hopfield利用神经网络求解TSP问题获得了成功,才使得连接主义重新受到人们的关注。1986 年,D.E. Rumelhart和J.L. McClelland主编了著名的《并行分布处理—认知微结构的探索》[8]一书,对PDP小组的研究工作进行了总结,轰动一时。特别是D.E. Rumelhart、G.E. Hinton和R.J. Williams重新发明了著名的BP算法,产生了非常大的影响。该算法可以说是最成功的神经网络学习算法,在当时迅速成为最流行的算法,并在很多应用中都取得了极大的成功[1]。在06年,Hinton将非监督学习用在NN中,使多层神经网络得到了比较好的效果,现在deep learning已经成为了机器学习里面的热点[2]。
2.Neural Network模型
NN有很多种不同的模型,这里学习一下最基本和最简单的BP网络,也称为MLP网络(multi-layer perceptrons)。BP网络架构如图所示,
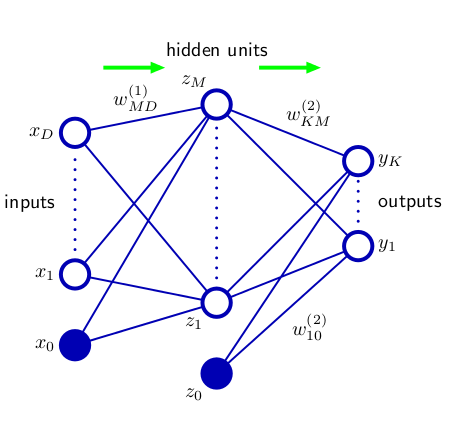
将上面的图公式化就是:
\[
y_k(x,w)=\sigma(\sum_{j=1}^{M}w_{k,j}^{(2)}h(\sum_{i=1}^{D}w_{j,i}^{(1)}x_i+w_{j,0}^{(1)})+w_{k,0}^{(2)})
\]
其中,第一层是input layer,中间是hidden layer,最后一层是output layer,通常称之为两层神经网络。上式中,$x$是输入变量;$w$是模型参数;$y$是输出的预测值;$h(x),\sigma(x)$是激活函数。在这里我们需要注意网络中节点和边的作用:
- 节点:输入层节点只接受输入即可,不用对输入做任何调整;隐藏层节点需要根据激活函数来对它连接的节点的线性组合,做变化;输出层节点需要针对不同的问题,选择恰当的激活函数。这样对于隐藏层和输出层来说,每个节点都有输入,输出。
- 边:节点之间的连接时层次化的,每一层接受前一层的每一个节点都会连接前一层的每一个节点,这也就是BP也被称作MLP(Multi-layer Perceptrons)的原因。注意这里$w_{j,i}$表示下一层的$j$节点,与上一层的$i$节点相连。
可以看出输出是输入的非线性函数。针对不同的问题,选择不同的$\sigma(x)$,具体可以参考[3]的p236。下面看一个具体的例子,结构图如下[注:图中蓝色的节点表示1]:
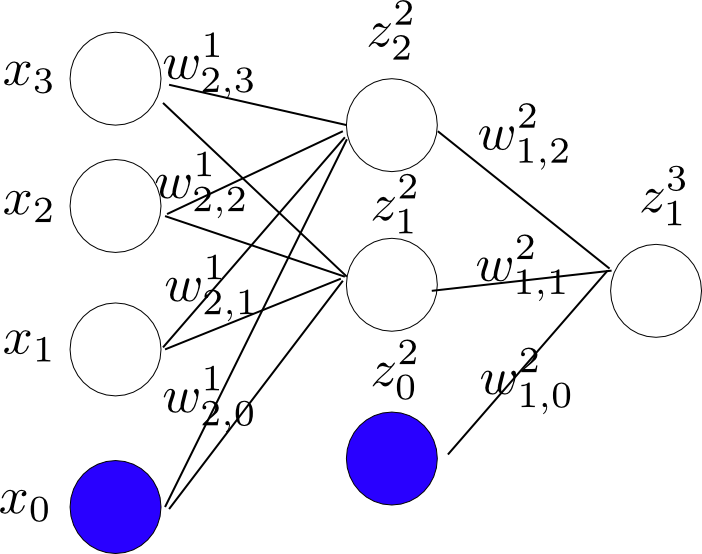
从图中,可以得出:
z_1^{(2)} = h(w_{10}^{(1)}x_0 + w_{11}^{(1)}x_1 + w_{12}^{(1)}x_2 + w_{13}^{(1)}x_3) \\
z_2^{(2)} = h(w_{20}^{(1)}x_0 + w_{21}^{(1)}x_1 + w_{22}^{(1)}x_2 + w_{23}^{(1)}x_3) \\
z_1^{(3)} = h(w_{10}^{(2)}z_0^{(2)} + w_{11}^{(2)}z_1^{(2)} + w_{12}^{(2)}z_2^{(2)} ) \\
\]
a^j=w^{j-1}z^{j-1}\\
z^j=h(a^j)
\]
3.模型训练
针对上述模型的误差函数分析,在NN用来处理回归问题时,与前面的linear regression model的分析过程完全一致,所以我们可以选择最小平方差(least square);处理分类问题时可以选择交叉熵误差函数(cross entropy )。
我们可以选择前面提到的sgd方法训练参数,但是由于$y$不再是关于参数的线性函数,所以梯度的求解不再像前面那么简单。求解梯度需要用到back propagation算法(ps:这也是这种网络称为BP网络的原因)。下面看一下BP具体算法的理论。
我们的目标是求出$\frac{\partial\mathbb E_n}{\partial w_{j,i}}$,从我们的模型假设可以看出$w_{j,i}$只与$a_j$相关,所以根据求导的链式法则,
\[
\frac{\partial\mathbb E_n}{\partial w_{j,i}}=\frac{\partial\mathbb E_n}{\partial a_j}\frac{\partial a_j}{\partial w_{j,i}}
\]
我们记:$\delta_j=\frac{\partial\mathbb E_n}{\partial a_j}$,称为该节点的错误(Error);因为$a_j=\sum_i w_{j,i}z$,所以可以得出,$\frac{\partial a_j}{\partial w_{j,i}}=z_i$,所以可以得出,
\[
\frac{\partial\mathbb E_n}{\partial w_{j,i}}=\frac{\partial\mathbb E_n}{\partial a_j}\frac{\partial a_j}{\partial w_{j,i}}=\delta_{j}z_{i}
\]
可以看出,$\mathbb E_n$相对$w_{j,i}$的导数是该边连接的上一层的开始节点的输出值乘以下一层结束节点的错误值(这也可以帮助我们理解后来更新参数的具体过程,网络上每一条边上的参数$W$是由它指向的错误来修正的)。网络中,每个节点的值输出值可以根据forward-propagation来容易的求解。下面看一下如何求解$\delta_j$。
对于$\delta$,对于输出层和隐藏层来说,求解不同。如果我们假设模型是回归问题,则对于输出层来说,可以得到:
\[\delta_j= y_j-t_j\]
对于隐藏层节点来说,再根据导数的链式法则,
\[
\delta_j=\frac{\partial\mathbb E_n}{\partial a_j}=\sum_k\frac{\partial\mathbb E_n}{\partial a_k}\frac{\partial a_k}{\partial a_j}
\]
从中可以看出,$\frac{\partial\mathbb E_n}{\partial a_k}=\delta_k$,所以,
\[
\delta_j=\frac{\partial\mathbb E_n}{\partial a_j}=\sum_k\delta_kh^{'}(a_j)w_{k,j}=h^{'}(a_j)\sum_k\delta_kw_{k,j}
\]
上面的求导过程用到了$a_k=\sum_jw_{k,j}h(a_j)$。这样我们就得到了一个$\delta$的递推式,就可以求出$\delta$了,这样导数也就可以求解了。
上面是理论推导,下面看个具体的例子,对我们上面那个具体的网络,看一下backpropagation的具体过程。
1.使用forward-propagation来求解网络中各个节点的值。具体如下图,
节点$z_2^2$:
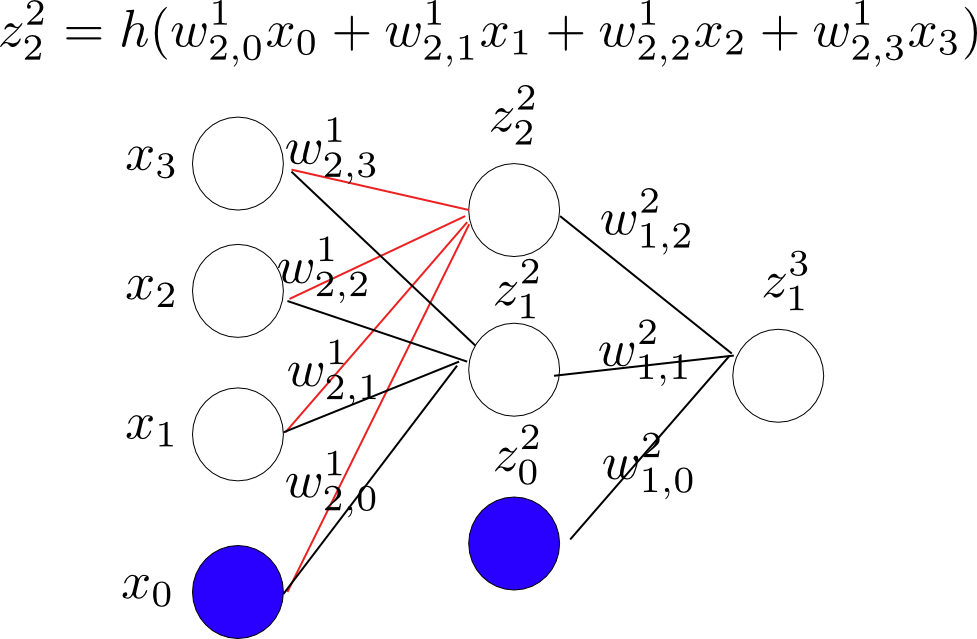
节点$z_1^2$:
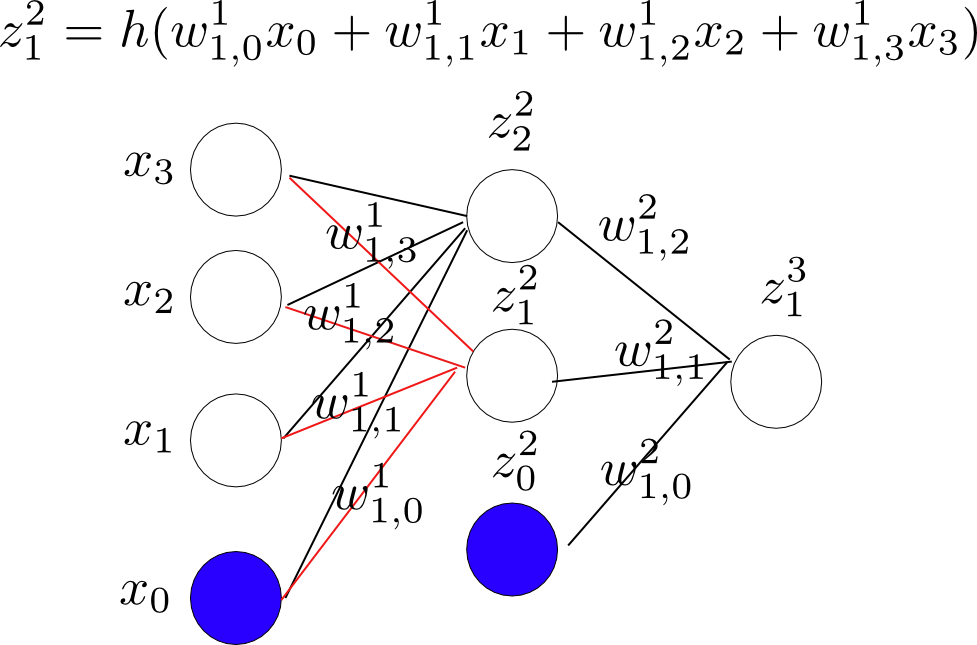
节点$z_1^3$:
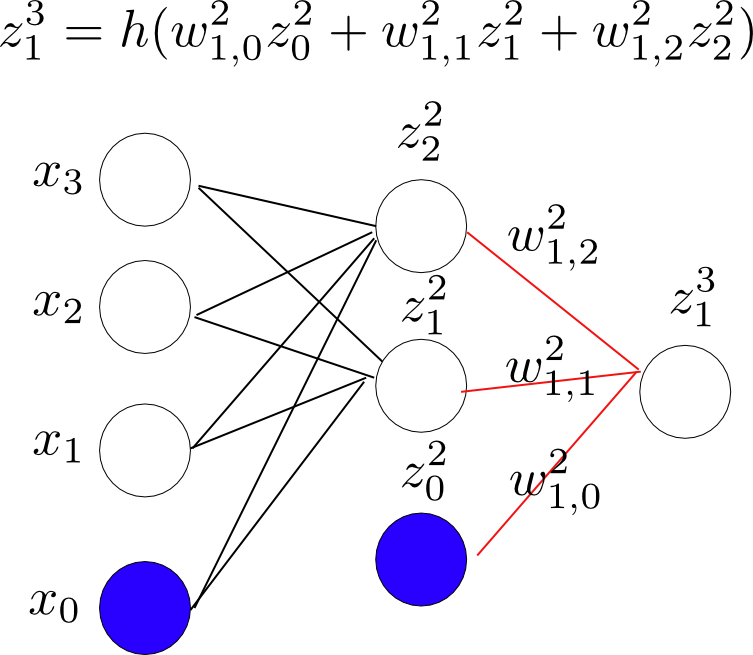
这样就完成了forward-propagation的过程,网络中各个节点的值就都求出来了。
2.下面就可以使用上面推到的公式,求解各个节点的错误值$\delta$了。
输出层$\delta$:
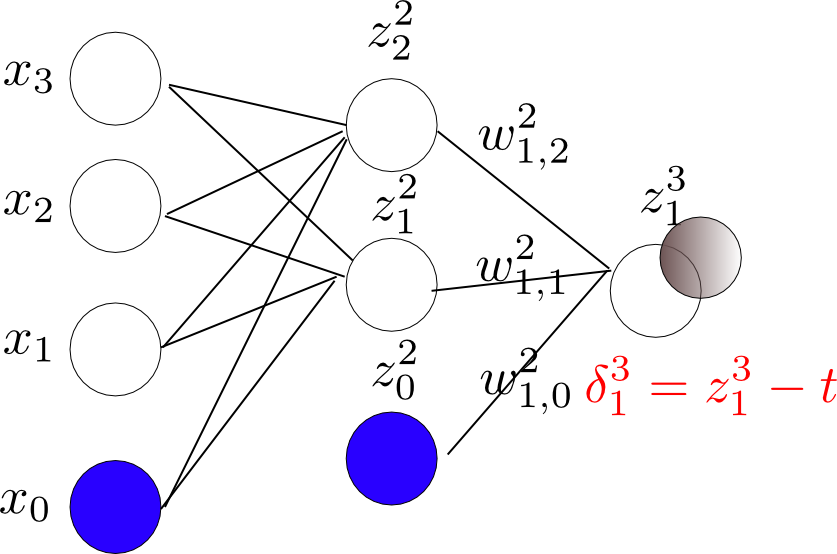
中间层$\delta$:
[更正24/10,2012]:下面图中的公式标注有误,$h'(z^i)$应为$h'(a^i)$.
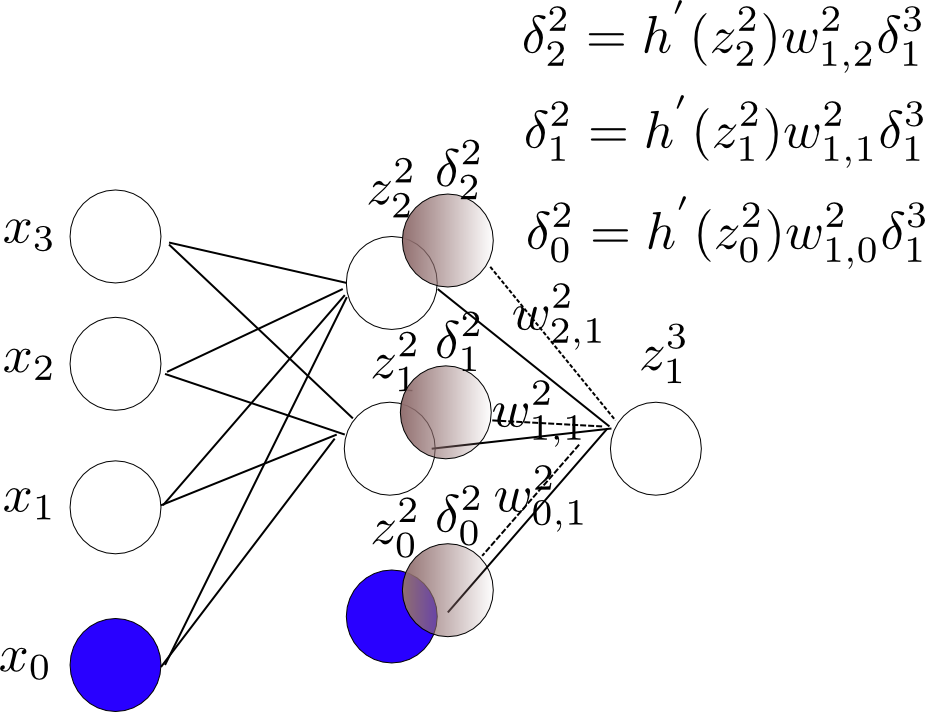
3.根据上面求出的$\delta$值就可以对网络中的参数$w$求偏导了。
上面使用BP算法,求得了目标函数对于参数的梯度值,下面利用梯度的值就可以用来优化目标函数,从而求出参数的值。如果我们直接使用batch gradient来求解,根据在“linear regression model”中提到的下面公式,
\begin{equation}
\theta = \theta - \eta\bigtriangledown p(\theta) = \theta-\eta\sum_{n=1}^{N}\bigtriangledown p_i(\theta)
\label{gradient}
\end{equation}
\]
现在都讲“BIG DATA”,每次更新参数的时候,我们都需要扫描一遍所有的数据,当数据很大,扫描数据的代价很大(尤其是如果没法全部的把数据载入到内存中,而要读写磁盘,IO的代价,可能是我们没法承受的),所以在一般情况下batch gradient不被使用;我们可以使用已经提到过的stochastic gradient desent,相比较batch gradient descent,sgd更新参数更频繁,如下面公式所示:
\[
\begin{equation} \theta = \theta-\eta \bigtriangledown p_{i}(\theta)
\label{sto_gradient}
\end{equation}
\]
对于每个训练样本,我们可以计算梯度,然后用来更新参数,但是sgd的一个问题就是它不能像batch gradient descent那样,保证可以收敛到局部的最优解。不过对于learning来说,这不是一个问题,毕竟我们不需要在training data上的最优解,我们更关注的是在test data上泛化的能力如何。介于两者之间的是mini-batch gradient descent,在更新参数的时候,不是选择全部,而是选择一部分的data计算梯度,从而用来更新参数,公式如下:
\[
\begin{equation}
\theta = \theta - \eta\bigtriangledown p(\theta) = \theta-\eta\sum_{n=1}^{B}\bigtriangledown p_i(\theta)
\label{gradient2}
\end{equation}
\]
上面式子中$B$表示mini-batch的大小,通常的取值范围是:2~200。mini-batch相对于online来说,一个明显的好处就是在可以使用矩阵计算来求解mini-batch上的梯度,从而加快运算的速度(可以使用GPU运算)。总起来说,三种方法在更新参数的频率上不同:
- batch:每次迭代,使用训练集中所有的数据计算梯度,更新参数;
- online:每次迭代,使用训练集中的一个样本计算梯度,更新参数;
- mini-batch:每次迭代,使用训练集合中一部分(大小为B)的数据计算梯度,更新参数;
下面是Hinton在coursera的NN课程上讲的几个注意的地方:
- 权值的初始化:一定要注意随机的初始值,来打破symmetry,所以$W$直接初始化为$0$,会非常的糟糕。ANG在他的课件上给了一个经验公式,来确定$W$随机取值的范围$[-\epsilon, \epsilon]$,其中$\epsilon$取值为:$\sqrt(\frac{6}{L_{in}+L_{out}})$,其中$L_{in},L_{out}$分别为输入和输出层的节点数目;
- 数据归一化(standarization):这样做的目的,可以使得误差函数近似‘碗装’,更好的使用梯度来优化目标函数。具体的可以参照Hinton在Lecture 6中的解释。
4.总结
这样我们就可以总结NN学习的基本过程[4]:
- 确定网络的结构,有几层网络,中间节点数目。输入层节点数目与特征维数一样;输出节点数目与类的个数一样;中间层一般有一层,如果有多层,有一样的节点数目。
-
训练过程:
- 初始化参数$w$。
- 使用forward-propagation的方式来计算中间节点的值和输出值。
- 实现cost function。
- 使用backward-propagation的方式计算cost function相对参数的偏导数。
- 使用随机梯度下降(或者是其他优化算法)计算参数。
当实现了forward-propagation和backward-propagation,可以在训练集合的每个实例上训练:
for i = 1:m, Perform forward propogation and backpropogation using example (x(i),y(i)) (Get activations a(l) and delta terms d(l) for l = 2,...,L
[引用]
[1]机器学习与数据挖掘。http://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/cccf07.pdf
[2]Neural Networks.http://en.wikipedia.org/wiki/Neural_network
[3]prml.http://book.douban.com/subject/2061116/
[4]https://share.coursera.org/wiki/index.php/ML:Neural_Networks:_Learning
[5]http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html一个很好的BP网络的实例
 评论 (0)
评论 (0)