webdancer's Blog
字符串算法
字符串的算法很多，下面讨论几个比较典型的与字符串匹配有关的算法。
1.LCS最长公共子序列
字符串的子序列是指从该字符串中删除一些字符（可以不删除），保持字符之间的相对位置不变，而得到的字符串；$A,B$之间的最大公共子序列是指求出$A,B$相同的子序列中，长度最长的那个。
输入：两个字符串$A,B$，长度为$m,n$
输出：字符串$A,B$的最长公共子序列
认识MD5
MD5是一种安全哈希算法（secure hash algorithm,SHA）;SHA是一种加密哈希函数（cryptographic hash function）;加密哈希函数是一种哈希函数(hash function); 哈希函数是一种函数。下面我们就看一下这些概念。
1.函数（function）
学习过离散数学，我们对函数并不陌生。不严格地说，在定义域上上的值x,都有值域上唯一的值y与之对应，这种映射关系成为函数。简单地说，函数可以将一些数值变换到另外一些数值（当然可以使本身）。注：数学上的函数与编程语言的函数还是有些不同，虽然在程序中的函数，给定输入（参数），可以得到输出（返回值）两者的范畴感觉还是不太一样。
2.哈希函数（hash function）
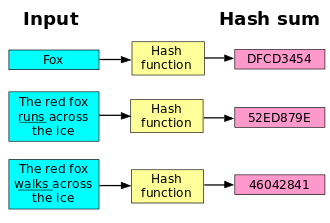
散列函数是一种从任何一种数据中创建小的数字“指纹”的方法。哈希函数得到的输出成为散列值。哈希函数是一种特殊的函数，当然满足函数的基本性质，即两个不同的散列值对应的输入时不同的。散列函数把消息或数据压缩成摘要，使得数据量变小，将数据的格式固定下来。不同的输入映射到相同的散列值称“碰撞”。哈希函数如下图所示：
哈希函数的主要应用有：
- 散列表。散列表是一种重要的数据结构，是哈希函数的一个重要应用。使用散列表能够快速的按照关键字查找数据记录。
- 加密。一个典型的加密单向函数是“非对称”的，并且由一个高效的散列函数构成。加密算法可以分为两类: 对称加密和非对称加密
- 错误校正。使用一个散列函数可以很直观的检测出数据在传输时发生的错误。在数据的发送方，对将要发送的数据应用散列函数，并将计算的结果同原始数据一同发送。在数据的接收方，同样的散列函数被再一次应用到接收到的数据上，如果两次散列函数计算出来的结果不一致，那么就说明数据在传输的过程中某些地方有错误了。
- 语音识别，Rabin-Karp 字符串搜索算法等。
3.加密哈希函数（Cryptographic hash function）
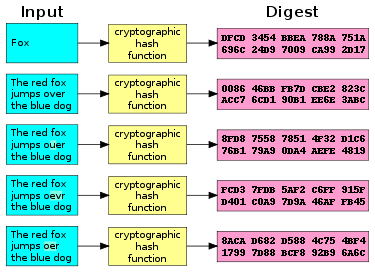
加密哈希函数是一种哈希函数，其满足哈希函数的基本性质：将一个大数据转为一个固定bit的字符串。其输入和输出分别成为：message（消息）和digest（摘要）。其中一个良好的加密哈希函数要求一下几点：
- 有消息容易计算摘要。
- 有摘要反向得到消息是不可行的（哈希函数不可逆，单向函数）
- 消息改变，摘要一定改变（哈希函数不碰撞）
- 两个不同的消息，对应不同的摘要（哈希函数不碰撞）
安全哈希函数如下所示：
应用：
- 文件或消息完整性验证。
- 文件或数据标识。比如git等代码管理系统使用sha1sum来区分不同内容。
4.安全哈希算法（secure hash algorithm,SHA）
安全散列算法是一种能计算出一个数位讯息所对应到的，长度固定的字串（又称讯息摘要）的算法。SHA家族的五个算法，分别是SHA-1、SHA-224、SHA-256、SHA-384，和SHA-512，由NSA所设计，并由NIST发布；是美国的政府标准。后四者有时并称为SHA-2。
python的hashlib模块中实现了上述五种SHA算法和更早的md5算法。
5.MD5
MD5即Message-Digest Algorithm 5用于确保信息传输完整一致。是计算机广泛使用的杂凑算法之一 ，主流编程语言普遍已有MD5实现。
MD5是一种安全哈希算法，但是MD5较老，散列长度通常为128位元，随着计算机运算能力提高，找到“碰撞”是可能的。在加密哈希函数中已经说过，一个良好的加密哈希函数应该不碰撞。2004年，王小云证明MD5数字签名算法可以产生碰撞。
为什么证明产生碰撞，MD5算法就失效了呢？以前不太理解，下面的解释还是比较清楚地。
根据密码学的定义，如果内容不同的明文，通过散列算法得出的结果（密码学称为信息摘要）相同，就称为发生了“碰撞”。散列算法的用途不是对明文加密，让别人看不懂，而是通过对信息摘要的比对，判断原文是否被篡改。所以说对摘要算法来说,它只要能找到碰撞就足以让它失效，并不需要找到原文。具一个例子， Linux的用户安全机制，只要得到用户密码文件（其中记录了密码的MD5），然后随便生成一个碰撞的原文（不一定要跟原密码相同），就可以用这个密码登录了。
参考：wikipedia
shuffling(洗牌)
Shuffling is a procedure used to randomize a deck of playing cards to provide an element of chance in card games. —wikipedia
To shuffle an array a of n elements (indices 0..n-1):
for i from n − 1 downto 1 do
j ← random integer with 0 ≤ j ≤ i
exchange a[j] and a[i]
python代码实现：
def fyshuffling(a):
for i in range(len(a)-1,0,-1):
j=random.randint(0,i)
a[i],a[j]=a[j],a[i]
2011山大免试研究生机试题
----------------以下仅提供了解体的思路，代码未完善，上机时有些题可以直接算出来的------------------------------
1.求两个正整数的最大公约数.
def gcd(a,b):
while b:
a,b=b,a%b
return a
2.令S=s1s2s3...s2n是一个符合规范的括号字符串。可以采用两种方式对S编码：
（1）一个整数序列P=p1p2...pn，其中pi是字符串S中第i个右括号前左括号的个数（记为P序列）；
（2）一个整数序列W=w1w2...wn，其中wi是字符串S中第i个右括号往左数遇到和它相匹配的左括号时经过的左括号个数（记为W序列).
要求：对于一个符合规范的括号字符串，将其P序列转化为W序列.
def translate( a ):
#stack
s=[]
b=[]
for i in range(len(a)):
if i==0:
for j in range(a[i]):
s.append('(')
b.append(1)
s.append(')')
b.append(1)
else:
for j in range(a[i]-a[i-1]):
s.append('(')
b.append(1)
s.append(')')
b.append(1)
c=[]
for m,v in enumerate(s):
count=0
if v==')':
for n in range(m-1,-1,-1):
if s[n]=='(':
count+=1
if s[n]=='(' and b[n]==1:
b[n]=0
break;
c.append(count)
for e in c:
print e ,
print '\n-----------'
3.有n个半圆形金属条c1,c2,c3...cn,半圆直径分别为l1,l2,l3...ln.(如图)问可否将这些金属环首尾相接形成一个大环.
要求:输入3组直径数据(组内数据之间已用逗号隔开,每组数据间已用分号隔开),判断这3组金属条各自是否可以首尾相接.针对每组数据，如果可以，输出Y，否则输出N.
def isconnect(a):
m=max(a)
s=0
first=True
for e in a:
if e!=m:
s+=e
if e==m and first:
first=False
elif e==m and not first:
s+=e
if m>s:
return False
else:
return True
4.设有一个由0和1组成的字符串b1b2……bn（bi为0或1）.由该字符串可以生成一个旋转矩阵B如下:
b1 b2 … bN−1 bN （第一行为原字符串，以下n-1行均由其前一行的串循环左移一位构成）
b2 b3 … bN b1
…
bN−1 bN … bN−3 bN−2
bN b1 … bN−2 bN−1
矩阵B的每一行可视为一个二进制数.对这n个二进制数由小到大排序形成矩阵C.
比如有一个二进制串00110，生成的旋转矩阵为
00110
01100
11000
10001
00011
对其排序得
00011（第一行的00011<第二行的00110<第三行的01100<......）
00110
01100
10001
11000
现在设有一个二进制串r经以上变换及排序后生成矩阵C1.
要求:输入一个二进制串，如果将其视为C1的最后一列,推测并输出C1的第一行数据.
例:输入10010 程序需要输出00011
def bwt(s):
assert '\0' not in s, "s CAN NOT contains ('\0')"
s+='\0'
table=sorted(s[i:]+s[:i] for i in range(len(s)))
r=[row[-1] for row in table]
return ''.join(r)
def ibwt(r):
table=['']*len(r)
for i in range(len(r)):
table=sorted(r[i]+table[i] for i in range(len(r)))
s=[row for row in table if row.endswith('\0')][0]
return s.rstrip('\0')
强连通分支
#!/usr/bin/python class Graph: def __init__(self,nv): self.v=nv self.e=0 self.adj=[] for ele in range(nv): self.adj.append([]) ele+=1 def insert(self,e): u=e[0] v=e[1] self.adj[u].append(v) #self.adj[v].append(u) self.e+=1 def dfs(self): global p global c global d global f global time global t p=[] c=[] d=[] f=[] t=[] for ele in range(self.v): ele+=1 p.append(-1) c.append(0) d.append(0) f.append(0) t.append(0) time=0 m=0 for elev in range(self.v): if c[elev] == 0: self.dfs_visit(elev,m) def dfs_visit(self,u,m): global time c[u]=1 t[u]=m time+=1 d[u]=time for v in self.adj[u]: if c[v] == 0: p[v]=u t[v]=m self.dfs_visit(v,m) c[u]=2 time+=1 f[u]=time '''def printpath(self,s,v): if s==v: print s, elif p[v]==-1: print 'no path', else: self.printpath(s,p[v]) print v,''' def scc(g): g.dfs() gt=Graph(g.v) for u in range(len(g.adj)): for v in g.adj[u]: gt.adj[v].append(u) u+=1 f1=[] for e in f: f1.append(e) for i in range(gt.v): p[i]=-1 c[i]=0 d[i]=0 f[i]=0 t[i]=0 print c time=0 global m m=0 for i in range(gt.v): v=max(f1) fi=f1.index(v) if c[fi] == 0: m+=1 gt.dfs_visit(fi,m) f1[fi]=-1 if __name__=='__main__': g=Graph(8) e=[(0,1),(1,2),(1,4),(1,5),(2,3),(2,6),(3,2),(3,7),(4,0),(4,5),(5,6),(6,5),(6,7),(7,7)] for each in e: g.insert(each) scc(g) print t for i in range(m+1): for v in range(g.v): if t[v]==i+1: print v, print '\n'
0/1背包的回溯法
解法：回溯法。
思路：在遍历的子集树的过程中，应该注意筛选出可行的解，同时当有更好的解时，不断地更新最优解。
#include<stdio.h>
#define N 4
int x[N];
int p[N];
int w[N];
int c;
int pmax;
int pcur;
int wcur;
int bound(int t){
int i,pr;
pr=pcur;
for(i=t;i<N;i++)
pr+=p[i];
if(pr>pmax)
return 1;
return 0;
}
void backtrace(int t){
int i;
if(t>=N){
if(pmax<pcur){
pmax=pcur;
for(i=0;i<N;i++)
printf("%d ",x[i]);
printf("\n");
}
}
else{
for(i=1;i>=0;i--){
x[t]=i;
if(i){
if(w[t]+wcur<=c){
wcur+=w[t];
pcur+=p[t];
backtrace(t+1);
wcur-=w[t];
pcur-=p[t];
}
}
else if(bound(t))
backtrace(t+1);
}
}
}
int main(){
c=7;
w[0]=3;
w[1]=5;
w[2]=2;
w[3]=1;
p[0]=9;
p[1]=10;
p[2]=7;
p[3]=4;
backtrace(0);
printf("the max :%d\n",pmax);
return 0;
}
8皇后问题的回溯解法
问题：在8X8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线（2条）上，问有多少种摆法。
解法：采用回溯算法。
#include<stdio.h>
#include<stdlib.h>
#define N 9
int x[N];
void vswap(int *pi,int *pj){
int tmp=*pi;
*pi=*pj;
*pj=tmp;
}
void out(int * x,int n){
int i;
for(i=1;i<n;i++)
printf("%d ",x[i]);
printf("\n");
}
void init(int *x,int n){
int i;
for(i=1;i<n;i++)
x[i]=i;
}
int bound(int t){
int i;
for(i=1;i<t;i++)
if(abs(x[i]-x[t])==abs(i-t)||x[t]==x[i])
return 0;
return 1;
}
void traceback(int t){
if(t>=N){
out(x,N);
}
else{
int i;
for(i=t;i<N;i++){
vswap(&x[t],&x[i]);
if(bound(t))
traceback(t+1);
vswap(&x[t],&x[i]);
}
}
}
int main(){
init(x,N);
traceback(1);
return 0;
}
运行：
gcc -o 8q 8q.c
结果：
./8q|wc -l
为：92.
回溯法
回溯法：从问题的某一种状态（初始状态）出发，搜索从这种状态出发所能达到的所有“状态”，当一条路走到“尽头”的时候（不能再前进），再后退一步或若干步，从另一种可能“状态”出发，继续搜索，直到所有的“路径”（状态）都试探过。这种不断“前进”、不断“回溯”寻找解的方法，就称作“回溯法”。
回溯算法：
- 形式化解的结构，根据形式描述，建立解树。解树的每个非叶子节点描述一类可行解，而叶子节点通常描述一个可行解。
- 利用深度优先搜索解空间。算法根据目标函数，确定节点所代表解的优化程度，当访问叶子节点时，解就唯一的确定了；访问中间节点时还没法唯一的确定，无法计算目标函数值。利用启发函数和分支定界，避免移动到不可能产生解的子空间。问题的解空间通常是在搜索问题的解的过程中动态产生的，这是回溯算法的一个重要特性。
解空间：
回溯算法的解空间一般分为：子集树和排列树。
子集树：二叉树来表示，较为熟悉。
排列树：第一层树有n个选择，第二层有n-1个选择，以此类推，直到叶子节点。
子集树和排列树都是“隐式图”。
子集树遍历的伪代码：
void backtrack(int t)
{
if(t>n)
output(x);
else
for(int i=0; i<=1; i++)
{
x[t] = i;
backtrack(t+1);
}
}
排列树遍历的伪代码：
void backtrack(int t)
{
if(t>n)
output(x);
else
for(int i=t; i<=n; i++)
{
swap(x[t], x[i]);
backtrace(t+1);
swap(x[t], x[i]);
}
}