webdancer's Blog

大数乘法，加法，除法运算 (转)

大数乘法，加法，除法

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

/*  写写大整数的一些算法,网上也可以找到，不过没有完整的
*   程序，于是写写比较完整的程序，发在Blog上
*/
#include <stdio.h>
#define MAXINT 1000
int compare(int a[],int b[]);
int bigplus(int a[],int b[],int c[]);
int bigsub(int a[],int b[],int c[]);
int bigmult(int a[],unsigned int b,int c[]);
int bigmult2(int a[],int b[],int c[]);
int bigdiv(int a[],unsigned int b,int c[],int *d); 
int bigdiv2(int a[],int b[],int c[],int d[]);
int main(int argc, char *argv[])
{
  int a[MAXINT]={10,5,4,6,5,4,3,2,1,1,1};     //被乘数或被除数 
  int b[MAXINT]={7,7,6,5,4,3,2,1};             //乘数或除数 
  int c[MAXINT],d[MAXINT];                    //c[]存放商，d[]存放余数 
  int div=1234;                               //小乘数或小除数 
  int k=0;
  int *res=&k;                                //小余数整数指针 
  bigplus(a,b,c); 
  bigsub(a,b,c); 
  bigmult(a,div,c); 
  bigmult2(a,b,c);
  bigdiv(a,div,c,res);
  bigdiv2(a,b,c,d);
  getchar();
  return 0;
}
int compare(int a[],int b[])          //比较大整数的大小 
{
    int i;
    if (a[0]>b[0]) return 1;          //比较a,b的位数确定返回值 
    else if (a[0]<b[0]) return -1;
    else                              //位数相等时的比较 
    {
        i=a[0];
        while (a[i]==b[i])            //逐位比较 
           i--;
        if (i==0) return 0;
        else if (a[i]>b[i]) return 1;
        else return -1;
    }
}
int bigplus(int a[],int b[],int c[])  //大整数加法 
{
    int i,len;
    len=(a[0]>b[0]?a[0]:b[0]);  //a[0] b[0]保存数组长度，len为较长的一个 
    for(i=0;i<MAXINT;i++)       //将数组清0 
        c[i]=0;
    for (i=1;i<=len;i++)        //计算每一位的值 
    {
        c[i]+=(a[i]+b[i]);
        if (c[i]>=10)
        {
           c[i]-=10;            //大于10的取个位 
           c[i+1]++;            //高位加1 
        }
    }
    if (c[i+1]>0) len++;
        c[0]=len;                //c[0]保存结果数组实际长度 
    printf("Big integers add: "; 
    for (i=len;i>=1;i--)
                printf("%d",c[i]); //打印结果 
        printf("\n";
    return 0;
}
int bigsub(int a[],int b[],int c[]) //大整数减法 
{
    int i,len;
    len=(a[0]>b[0]?a[0]:b[0]);  //a[0]保存数字长度，len为较长的一个 
    for(i=0;i<MAXINT;i++)       //将数组清0 
        c[i]=0;
    if (compare(a,b)==0)        //比较a,b大小 
    {
       printf("Result:0";
       return 0; 
    }
    else if (compare(a,b)>0)
    for (i=1;i<=len;i++)        //计算每一位的值 
    {
        c[i]+=(a[i]-b[i]); 
        if (c[i]<0)
        {
           c[i]+=10;            //小于0的原位加10 
           c[i+1]--;            //高位减1 
        }
    }
    else
        for (i=1;i<=len;i++)        //计算每一位的值 
        {
        c[i]+=(b[i]-a[i]); 
        if (c[i]<0)
        {
           c[i]+=10;            //小于0原位加10 
           c[i+1]--;            //高位减1 
        }
        }
    while (len>1 && c[len]==0)  //去掉高位的0 
        len--;
    c[0]=len;
    printf("Big integers sub= ";
    if (a[0]<b[0]) printf("-";
    for(i=len;i>=1;i--)         //打印结果 
        printf("%d",c[i]);
    printf("\n";
    return 0;
}
int bigmult(int a[],unsigned int b,int c[])//高精度乘以低精度 
{
    int len,i;
    for (i=0;i<MAXINT;i++)                  //数组清0 
      c[i]=0;
    len=a[0];
    for(i=1;i<=len;i++)                     //对每一位计算 
    {
       c[i]+=a[i]*b;
       c[i+1]+=c[i]/10;
       c[i]%=10;
    }
    while (c[++len]>=10)                    //处理高位 
    {
       c[len+1]=c[len]/10;
       c[len]%=10;
    }
    if (c[len]==0) len--;                   //处理高进位为0情况
    printf("Big integrs multi small integer: "; 
    for (i=len;i>=1;i--)
        printf("%d",c[i]);
    printf("\n"; 
}
int bigmult2(int a[],int b[],int c[])      //高精度乘以高精度 
{
    int i,j,len;
    for (i=0;i<MAXINT;i++)                  //数组清0 
        c[i]=0;
    for (i=1;i<=a[0];i++)                  //被乘数循环 
      for (j=1;j<=b[0];j++)                //乘数循环 
      {
         c[i+j-1]+=a[i]*b[j];              //将每一位计算累加 
         c[i+j]+=c[i+j-1]/10;              //将每一次结果累加到高一位 
         c[i+j-1]%=10;                     //计算每一次的个位 
      }
   len=a[0]+b[0];                          //取最大长度 
   while (len>1 && c[len]==0)              //去掉高位0 
      len--;
   c[0]=len;
   printf("Big integers multi: ";
   for (i=len;i>=1;i--)                    //打印结果 
      printf("%d",c[i]);
   printf("\n";  
}
int bigdiv(int a[],unsigned int b,int c[],int *d) //高精度除以低精度 
{                                           //a[] 为被乘数,b为除数,c[]为结果,d为余数 
    int i,len;                               
    len=a[0];                          //len为a[0]的数组长度  
    for (i=len;i>=1;i--)
    {
       (*d)=10*(*d)+a[i];                        //计算每一步余数 
       c[i]=(*d)/b;                           //计算每一步结果 
       (*d)=(*d)%b;                              //求模余数 
    } 
    while (len>1 && c[len]==0) len--;        //去高位0
    printf("Big integer div small integer: "; 
    for (i=len;i>=1;i--)                    //打印结果 
      printf("%d",c[i]);
    printf("\tArithmetic compliment:%d",*d); 
    printf("\n"; 
}
int bigdiv2(int a[],int b[],int c[],int d[])  //高精度除以高精度 
{
   int i,j,len;
   if (compare(a,b)<0)                        //被除数较小直接打印结果 
   {
     printf("Result:0";
     printf("Arithmetic compliment:";
     for (i=a[0];i>=1;i--) printf("%d",a[i]);
     printf("\n";
     return -1;            
   }
   for (i=0;i<MAXINT;i++)                     //商和余数清0 
   {
      c[i]=0;
      d[i]=0;
   }
   len=a[0];d[0]=0;
   for (i=len;i>=1;i--)                       //逐位相除 
   {
      for (j=d[0];j>=1;j--)
        d[j+1]=d[j];
      d[1]=a[i];                              //高位*10+各位 
      d[0]++;                                 //数组d长度增1 
      while (compare(d,b)>=0)                 //比较d,b大小 
      {
            for (j=1;j<=d[0];j++)              //做减法d-b 
            {
                d[j]-=b[j];
                if (d[j]<0)
                {
                   d[j]+=10;
                   d[j+1]--;
                }
            }
                while (j>0 && d[j]==0)        //去掉高位0 
                      j--;
                d[0]=j;
            c[i]++;                           //商所在位值加1 
      }
   }
   j=b[0];
   while (c[j]==0 && j>0) j--;                //求商数组c长度 
     c[0]=j;
   printf("Big integers div result: "; 
   for (i=c[0];i>=1;i--)                      //打印商 
     printf("%d",c[i]);
   printf("\tArithmetic compliment: ";       //打印余数 
   for (i=d[0];i>=1;i--)
     printf("%d",d[i]);
   printf("\n";
}

trie tree （转）

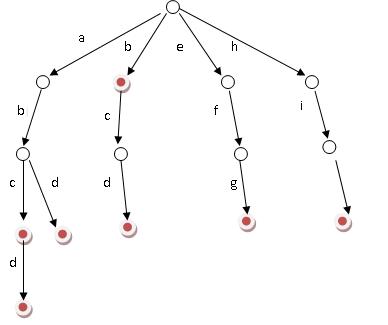
Trie,又称字典树、单词查找树,是一种树形结构，用于保存大量的字符串。它的优点是：利用字符串的公共前缀来节约存储空间。

相对来说,Trie树是一种比较简单的数据结构.理解起来比较简单,正所谓简单的东西也得付出代价.故Trie树也有它的缺点,Trie树的内存消耗非常大.当然,或许用左儿子右兄弟的方法建树的话,可能会好点.

其基本性质可以归纳为：
1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。

其基本操作有:查找插入和删除,当然删除操作比较少见.我在这里只是实现了对整个树的删除操作,至于单个word的删除操作也很简单.

搜索字典项目的方法为：

(1) 从根结点开始一次搜索；

(2) 取得要查找关键词的第一个字母，并根据该字母选择对应的子树并转到该子树继续进行检索；

(3) 在相应的子树上，取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。

(4) 迭代过程……

(5) 在某个结点处，关键词的所有字母已被取出，则读取附在该结点上的信息，即完成查找。
其他操作类似处理.

    <span style="font-family: verdana,geneva,sans-serif;">  Name: Trie树的基本实现 
Author: MaiK 
Description: Trie树的基本实现 ,包括查找 插入和删除操作*/
#include<algorithm>
#include<iostream>
using namespace std;
 
const int sonnum=26,base='a';
struct Trie
{
    int num;//to remember how many word can reach here,that is to say,prefix
    bool terminal;//If terminal==true ,the current point has no following point
    struct Trie *son[sonnum];//the following point
};
Trie *NewTrie()// create a new node
{
    Trie *temp=new Trie;
    temp->num=1;temp->terminal=false;
    for(int i=0;i<sonnum;++i)temp->son[i]=NULL;
    return temp;
}
void Insert(Trie *pnt,char *s,int len)// insert a new word to Trie tree
{
    Trie *temp=pnt;
    for(int i=0;i<len;++i)
    {
        if(temp->son[s[i]-base]==NULL)temp->son[s[i]-base]=NewTrie();
        else temp->son[s[i]-base]->num++;
        temp=temp->son[s[i]-base];
    }
    temp->terminal=true;
}
void Delete(Trie *pnt)// delete the whole tree
{
    if(pnt!=NULL)
    {
        for(int i=0;i<sonnum;++i)if(pnt->son[i]!=NULL)Delete(pnt->son[i]);
        delete pnt; 
        pnt=NULL;
    }
}
Trie* Find(Trie *pnt,char *s,int len)//trie to find the current word
{
    Trie *temp=pnt;
    for(int i=0;i<len;++i)
        if(temp->son[s[i]-base]!=NULL)temp=temp->son[s[i]-base];
        else return NULL;
    return temp;
} 
</span>