webdancer's Blog
求中位数
在统计学中,中位数代表一个样本中的一个数值,其可将数值集合划分为相等的上下两部分。
实数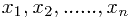 按大小顺序(升序,降序皆可)排列为
按大小顺序(升序,降序皆可)排列为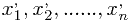 ,实数数列
,实数数列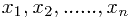 的中位数
的中位数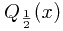 为:
为:
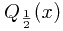 =
=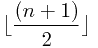
明确了概念后我们可以来解决怎么找中位数了。
算法1:按照定义所说的,首先排序,然后直接返回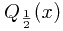 即可。
即可。
算法2:在《算法导论》中介绍了如何可以在期望线性时间找到中位数。
思想是:1.按照快排的思想,不断的随机分割。
2.如果随机分割的返回值恰是我们找的,可以返回该位置的数。
3.如果不满足,比较一下返回值与我们找的位置的大小,递归的进行下去,直到满足1.
算法3:
思想是: 1.利用快速排序的思想,不断的的分割。不过没有用递归。
用python实现了一下上面的算法,结果:
| algorithm1(ms) | algorithm2(ms) | algorithm3(ms) | |
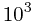 |
0 | 0 | 0 |
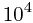 |
9 | 19 | 20 |
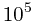 |
140 | 120 | 70 |
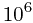 |
2149 | 1689 | 780 |
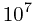 |
27480 | 21479 | 12480 |
参考:
1.http://zh.wikipedia.org/wiki/%E4%B8%AD%E4%BD%8D%E6%95%B0
2.算法导论。
递归
对于递归算法,基本没有什么理解,但是有时候递归的用处还是很多的。记录几个例子。
1.用递归的方法,写函数itoa(n,s),将整数转为字符串。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | int i;void itoa(int n,char s[]){ if(n/10) itoa(n/10,s); else{ i=0; if(n<0) s[i++]='-'; } s[i++]=n%10+'0'; s[i]='\0';} |
2.用递归方法,写函数reverse1(s),将字符串倒置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | void swap(char *i,char *j){ char tmp; tmp=*i; *i=*j; *j=tmp;}void reverse0(char s[],int i,int n){ int j; j=n-(i+1); if(i<j){ swap(&s[i],&s[j]); reverse0(s,++i,n); }}void reverse1(char s[]){ reverse0(s,0,strlen(s));} |
3.Fibonacci数列的递归实现。
1 2 3 4 5 6 | int fibonacci(int n){ if(n<2) return n; else return fibonacci(n-1)+fibonacci(n-2);} |
4.求最大公约数。
1 2 3 4 5 6 | int gcd(int x,int y){ if(y==0) return x; else return gcd(y,x%y);} |
递归:函数不断调用自身,直到遇到结束条件停止。
代码简洁,容易理解。但是,递归过程会消耗大量的栈空间,不适合嵌入式系统或者内核态编程。