linear regression model - webdancer's Blog

linear regression model

webdancer posted @ 2013年2月28日 20:36 in machine learning with tags Machine learning , 4814 阅读

机器学习算法有很多，有的非常复杂，本身需要的计算机基础要好。模型的构建和求解，需要概率论，信息论，高等数学，线性代数等等学科知识的理论支撑，所以对我们的数学知识要求会比较高。这还只是模型的构建，而到了具体编程方面，所需要的数值算法的要求也比较高。这里看一下最简单，最基本的linear regression model(线性回归模型)。文章的思路是首先学习线性回归模型是什么？然后在学习求解参数的一种点估计方法——最大似然估计和求解最优化问题的导数法和随机梯度下降的方法。

regression

就像在"概率"那篇文章提到的，机器学习的目的，一般来说，就是找一个函数$f:\mathcal{X} \rightarrow \mathcal{Y}$。在regression问题中，$\mathcal{Y}$是连续的，一般属于$\mathbb{R}$，比如我们要根据某个人烟龄来预测他的能活得岁数；根据过去几天的温度，预测未来几天的温度等。我们关心模型具体的输出值，这些值都是有具体的意义的。

例如，我们根据根据人的身高，来预测他的体重。数据集使用'machine learning for hackers'中提供的数据集。前十个数据点如下（csv格式），使用R提供的‘lm’方法，很容易做linear regression。：

"Gender","Height","Weight"
"Male",73.847017017515,241.893563180437
"Male",68.7819040458903,162.310472521300
"Male",74.1101053917849,212.7408555565
"Male",71.7309784033377,220.042470303077
"Male",69.8817958611153,206.349800623871
"Male",67.2530156878065,152.212155757083
"Male",68.7850812516616,183.927888604031
"Male",68.3485155115879,167.971110489509
"Male",67.018949662883,175.92944039571

heights.weights <- read.csv(file.path('data',
                                      '01_heights_weights_genders.csv'),
                            header = TRUE,
                            sep = ',')

ggplot(heights.weights, aes(x = Height, y = Weight)) +
  geom_point() +
  geom_smooth(method = 'lm')

fitted.regression <- lm(Weight ~ Height,
                        data = heights.weights)

linear regression model

上面我们用R进行了简单的分析，接下来看一下具体的理论。
线性回归模型是一种简单的统计模型，结构简单，$\mathcal{X}$与$\mathcal{Y}$是线性关系。虽然简单，对于我们理解后面的一些概念非常重要。线性回归是什么呢？简单来说，回归就是由一堆数来预测出一堆我们感兴趣的数。就如上面说的，回归模型的输出是连续的数值，这些数值通常就是我们需要的，比如预测大学的排名；这区别于以后的我们要学习的分类问题，分类模型的输出时离散的，通常分类的离散数值只是一些符号代表，没有实际的意义。下面从最简单的单变量线性回归模型说起，再拓展到多变量的模型。

单变量线性模型用到的一些符号：已知含有$N$个观测变量$x$以及对应的目标变量$y$的数据集合，记作：$\\{(x^1,y^1),(x^2,y^2),\dots.,(x^N,y^N)\\}$，其中第$i$个变量写为$(x^i,y^i)$。预测新的$x$的目标值$\hat{y}$。顾名思义，线性回归也就是说$y$与$x$之间有线性关系，即目标值是输入值的线性组合。线性回归的模型假设(hypothesis)为：

\[
\begin{equation}
\hat{y}=\theta_{0}+\theta_{1}x
\label{univar_lm}
\end{equation}
\]

其中，$x$为模型输入变量，$\hat{y}$为模型预测的目标变量值的近似，$\theta_{0},\theta_{1}$为模型参数。下面我们的目标就是如何求解模型中的参数，来确定模型。

[注：模型假设就是对输入变量和输出变量之间的关系的假设，是我们对数据间关系的认识]

优化的目标函数：直观上衡量模型好坏就是输出变量$\hat y$与目标变量$y$相差的程度，两者越接近，则越能反映$y$与$x$之间的关系。[注：这里我们的一个基本的假设就是对过去观测很好的模型，对将来的新到的变量也会很好，认为在训练集上一个高的准确率的模型自然会在以后的预测时的效果好。在后面我们会看到，这个假设是存在问题的，会存在Overfitting的现象]损失函数(loss function）可以作为我们求解模型的参数的方法，函数如下：

\[
\begin{equation}
\mathbb E=\frac{1}{2}\sum_{n=1}^{N}\{y^{(n)}-\hat{y}^{(n)}\}^2
\label{ls_error}
\end{equation}
\]

根据公式的数学意义我们可以看到，$\mathbb E$值越小，假设越好，这种方法就是很常见的最小二乘估计法。[注：其实很多模型都会用得到这种基本的方法]下面的工作就是来最小化$\mathbb E$。

现在我们对线性模型有了一个比较直观的印象，知道了什么是线性模型，得到一个优化的目标函数求解参数。这也是机器学习的一般过程：提出模型，根据假设得到一个最优化问题，求解最优化参数，最后评估模型。

下面来看一下多变量的线性回归模型：已知含有$N$个观测变量$X$，以及对应的目标变量$y$的数据集合，记作：$\\{(X^1,y^1),(X^2,y^2),\dots.,(X^N,y^N)\\}$,其中第$i$个变量写为$(X^i,y^i)$。预测新的$X$的目标值$\hat{y}$。我们线性回归的模型假设为：

\[
\begin{eqnarray}
\hat{y}&=& \theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\dots+\theta_{D}*x_{D}\\
\nonumber &=& \theta^{T}X
\label{mulvar_lm}
\end{eqnarray}
\]

其中，$X=(x_0,x_1,x_2,\dots,x_D)^{T}$为模型输入变量，$\hat{y}$为模型输出变量，$\theta=(\theta_{0},\theta_{1},\dots,\theta_D)$为参数，这样模型是关于输入$X$和参数$\theta$的线性函数。这样我们把$N$个观测变量$X$的数据集收集在一个矩阵中$\mathbf X$中，记作：

\[
\mathbf X =
\begin{bmatrix}
X_1^1 & X_1^2 & \dots & X_1^N \\
X_2^1 & X_2^2 & \dots & X_2^N \\
\vdots & \vdots & \ddots & \vdots \\
X_D^1 & X_D^2 & \dots & X_D^N
\end{bmatrix} = \begin{bmatrix}
1 & 1 & \dots & 1 \\
X_1^1 & X_1^2 & \dots & X_1^N\\
\vdots & \vdots & \ddots & \vdots \\
X_D^1 & X_D^2 & \dots & X_D^N
\end{bmatrix}
\]

矩阵中行数代表了特征数，列数代表数据集合中实例的数目。

对模型引入“基函数”，这样模型仅是相对于参数的线性模型，而不是相对于输入的线性模型，从而使模型增强。原来$y$与$X$是只能是线性关系，引入基函数后，$y$与$X$是非线性的情况也可以做处理了。模型假设如下：

\[
\begin{equation}
\hat{y}= \theta_{0}+\theta_{1}\phi_{1}(X)+\dots+\theta_{M}\phi_{M}(X)
\label{mulvar_lbm}
\end{equation}
\]

我们可以看到，通过引入“基函数”，参数数目由$D$变成了$M$，基函数的作用就是使输入空间变到了另外一个空间。

假设用向量表示形式为：

\[
\begin{equation}
\hat{y}=\theta^{T}\phi(X)
\label{mulvar_lbm_vec}
\end{equation}
\]

其中，$\theta=(\theta_0,\theta_1,\dots,\theta_M)$，$\phi=(1,\phi_1,\dots,\phi_M)$。

在理解“基函数”的作用的过程中，可能会出现问题。这里我们看一下基函数的作用：

由前面基函数的定义，它是将整个变量$X$，一个向量转化为一个标量(在wikipedia上的模型与我们这里的模型有些不同)。在实际的模式识别应用中，我们会对原始的数据进行一些预处理或是特征提取，原始的数据可以看做$X$，而处理后的数据看做$\phi(X)$。
实际处理问题时怎么对原始数据进行处理时非常灵活的。基函数的选取对于我们模型的讨论没有影响，所以后面我们将 $\phi(X)=X$来进行讨论。所以我们应该没有必要对这里的定义过于纠结，要关注模型。

Maximum Likelihood

那么最小二乘法背后有什么数学原理吗？我们可以从概率统计角度来进行解释。下面看一下用Maximum Likelihood方法，来解释多变量线性回归模型。我们的模型可能不能准确的确定目标变量，所以目标变量与模型输出变量之间存在噪声，两者关系写成如下等式：

\[
\begin{equation}
y=\hat{y}+\epsilon
\label{tarvar}
\end{equation}
\]

其中，$\epsilon$为噪声值，假设其为高斯噪声，符合高斯分布$\mathcal N(\epsilon|0,\beta)$。那么变量$y$的分布函数为：

\[
\begin{equation}
p(y|X,\theta,\beta)=\mathcal N(y|\hat{y},\beta)
\label{tar_dis}
\end{equation}
\]

已知训练集：输入为$\mathbf X=\{X^1,X^2,\dots,X^N\}$,对应的目标值为：$Y=(y^1,y^2,\dots,y^N)$。我们假定$N$个观测变量符合独立同分布(i.i.d.)，则似然函数如下：

\[
\begin{equation}
p(Y|\mathbf X,\theta,\beta)=\prod_{n=1}^N\mathcal N(y^{(n)}|\hat{y}^{(n)},\beta)
\label{tar_dis_total}
\end{equation}
\]

为了计算方便，取对数，得到对数似然函数，

\[
\begin{equation}
\begin{split}
lnp(Y|\mathbf X,\theta,\beta) &= \sum_{n=1}^Nln\mathcal N(y^{(n)}|\hat{y}^{(n)},\beta)
\label{ml_final}\\
&= \sum_{n=1}^Nln\mathcal N(y^{(n)}|\theta^{T}X^{(n)},\beta)\\
&= \frac{N}{2}ln\beta-\frac{N}{2}ln2\pi-\frac{\beta}{2}\sum_{n=1}^{N}\{y^{(n)}-\theta^{T} X^{(n)}\}^2
\end{split}
\end{equation}
\]

下面要做的就是最优化参数$\beta,\theta$使得似然函数取最大值，这就是最大似然方法的含义。而且可以看出上面式子的第三部分与最小平方和误差函数形式是一致的，这也从概率的角度解释了最小平方误差函数。

下面我们看一下最优化似然函数的方法：Normal Equation,gradient descent，stochastic gradient descent。首先来看以下上面式子关于$\beta,\theta$的导数。上式关于$\beta$的一次函数，关于$\theta$的二次函数，可以采用求导的方法来得到一个最大值。分别就似然函数相对于参数$\theta,\beta$的偏导数：

\[
\begin{equation}
\begin{split}
\frac{\partial}{\partial\theta}ln(p)&= \frac{\beta}{2}\sum_{n=1}^{N}\{(y^{(n)}
-\theta^{T} X^{(n)})(X^{(n)})\} \\
&= \frac{\beta}{2}\mathbf X(Y- \mathbf X \theta)
\end{split}
\end{equation}
\]

\[
\begin{equation}
\frac{\partial}{\beta}ln(p) = \frac{N}{2\beta}-\sum_{n=1}^{N}\{y^{(n)}-\theta^{T}X^{(n)}\}
\end{equation}
\]

然后让表达式都为0,得到一个二元方程组。解这个二元方程组，得到使最大的参数$\theta_{ml},\beta_{ml}$。$\beta$的值好求，求出$\theta$后带入即可。下面看一下求解$\theta$的方法。

normal equation

通过上面的式子可以看到，我们可以很容易使用矩阵计算，求出$\theta$的封闭解。式子为：

\[
\theta=(\mathbf X^{T}\mathbf X)^{-1}\mathbf XY
\]

greadient descent

梯度下降算法基于：函数在某点$x$处可微，那么函数在$x$处沿着梯度相反的方向下降最快。在机器学习算法中，最小化的目标函数通常

具有下面的形式：

\[
\begin{equation}
p(\theta)=\sum_{n=1}^{N}p_i(\theta)
\label{obj_gen}
\end{equation}
\]

梯度下降算法通常完成下面的迭代：

\[
\begin{equation}
\theta = \theta - \eta\bigtriangledown p(\theta) = \theta-\eta\sum_{n=1}^{N}\bigtriangledown p_i(\theta)
\label{gradient}
\end{equation}
\]

其中，$\eta$称为学习速率。所以在求解$\theta$的时候，只要初始化一个$\theta$值，然后不断的进行迭代即可。在进行梯度下降的时候Ang的ML课程里面提到了三个使用的技巧[3]:

归一化。对训练数据进行归一化，可以提高学习的速度，减少迭代次数。
收敛。可以通过观察每次的costfunction 的值或是设定收敛条件来看是否收敛。
学习速率的选择。当不收敛的时候可以减少$\eta$的值，通常按照3的倍数减少。

stochastic gradient descent

上面的梯度下降算法是一种batch方法，一次迭代的时候使用了所有的数据。我们可以可以近似为下面形式：

\[
\begin{equation} \theta = \theta-\eta \bigtriangledown p_{i}(\theta)
\label{sto_gradient}
\end{equation}
\]

这时候的算法，一次迭代只需要一个数据即可，所以是一种sequential的方法。

下面是伪代码[2]

initialize the parameter vectors $\theta,\eta$

REPEAT

Randomly shuffle examples in the training set

FOR $i = 1 \to N$

$\theta = \theta-\eta \bigtriangledown p_i(\theta)$

ENDFOR

UNTIL convenge to some criterion

其中，shuffle是“洗牌”的意思，顾名思义，就是打乱数据集原来数据的顺序。其中比较常用的shuffle algorithm有

Fisher–Yates shuffle。通过随机梯度下降可以很容易的计算出$\theta$,然后在根据计算$\beta$值。

模型扩展

Regularization 。使用最小二乘进行求解，可能出现过拟合的问题，所以可以使用Regularization来拓展线性模型，添加一个惩罚项。常见的有两种：Ridge 和 Lasso。数学公式如下：

\[
\mathbb E=\frac{1}{2}\sum_{n=1}^{N}\{y^{(n)}-\hat{y}^{(n)}\}^2+\frac{1}{2}\lambda \sum_{j=1}^{M}|w_j|^q
\]

其中，对于Ridge方法来说，$q=2$；对于Lasso 来说，$q=1$，$\lambda$是用来平衡这两项的参数。可以看出，两种方法只是惩罚项不同，Ridge添加了一个$\ell_2$ regularizer，而Lasso则添加了一个$\ell_1$ regularizer。但是却有不同的性质。其中Lasso有一个很好的性质就是它可以得出一个稀疏模型（sparse）。关于为什么会Lasso容易产生稀疏解，有一个直观的解释。

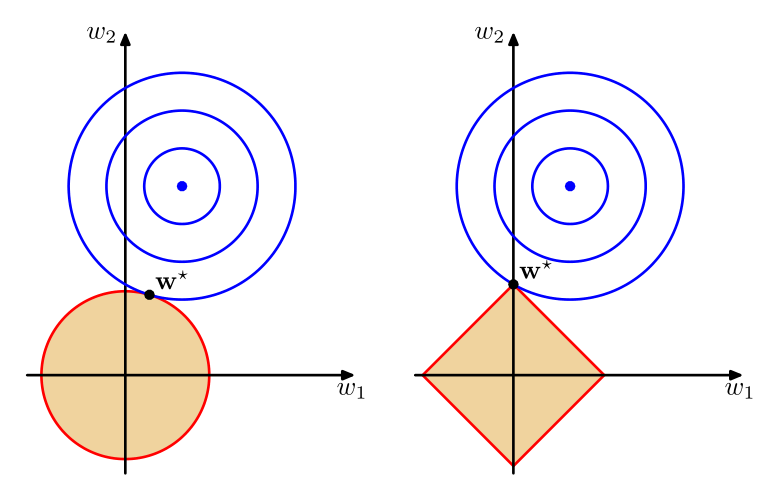
图中，左边为Ridge，右边为Lasso，参数解为两个图形相交的地方。可以看到Lasso的最优解容易产生稀疏解。而且我们还可以把这两种结合起来，称为”Elastic Net“，数学公式如下：

\[
\mathbb E=\frac{1}{2}\sum_{n=1}^{N}\{y^{(n)}-\hat{y}^{(n)}\}^2+\frac{1}{2}\lambda_1 \sum_{j=1}^{M}|w_j|+\frac{1}{2}\lambda_2 \sum_{j=1}^{M}|w_j|^2
\]

当然还有其他的扩展。我们可以使用概率统计的观点来解释Regularization，就是把原来的MLE拓展到MAP，正则项则对应我们参数的先验。

Bayesian.根据我们使用MLE求解，可以很自然的进行拓展到Bayesian，不把参数值，而作为随机变量，去估计它的后验概率分布，然后使用这个概率分布来得到预测的分布，这里就不详细介绍了。

实例

数据集：使用的scikit-learn中自带的数据集boston，关于数据的详细内容，可以参照查看http://archive.ics.uci.edu/ml/datasets/Housing。

代码：

结果：

使用MSE（Mean square error）来衡量预测，结果如下：

linear regression, mse : 33.075626
ridge regression, mse : 32.657563
lasso regression, mse : 29.705073
elastic net regression, mse : 19.523192

可以看出，elastic net取得了最后的结果，而linear regression 的结果最差，这说明增加惩罚项，的确可以提高预测的准确性。

[引用]

1.pattern recognition and machine learning.

2.wikipedia stochastic gradient descent.

3.https://share.coursera.org/wiki/index.php/ML:Linear_Regression_with_Multiple_Variables