上次记录了，0/1背包问题动态规划的递归实现，下面记录一下也是动态规划的非递归实现。主要是对f函数结果的记录，使得不用像递归中的重复计算。

#include<stdio.h>
#include<stdlib.h>

#define max(a,b) (a)>(b)?(a):(b)
#define min(a,b) (a)<(b)?(a):(b)
#define N 3
#define C 116

int p[N+1];
int w[N+1];
int f[N+1][C+1];
int x[N+1];
void bag(){
    int y,ymax,i;

    ymax=min(w[N]-1,C);
    for(y=0;y<ymax;y++)
        f[N][y]=0;
    for(y=w[N];y<C;y++)
        f[N][y]=p[N];

    for(i=N-1;i>1;i--){
        ymax=min(w[i]-1,C);
        for(y=0;y<ymax;y++)
            f[i][y]=f[i+1][y];
        for(y=w[N];y<C;y++)
            f[i][y]=max(f[i+1][y],f[i+1][y-w[i]]+p[i]);
    }
    f[1][C]=f[2][C];
    
    if(C>w[1])
        f[1][C]=max(f[2][C],f[2][C-w[1]]+p[1]);
}

void traceback(){
    int i,c;
    
    c=C;
    for(i=1;i<N;i++)
        if(f[i][c]==f[i+1][c])
            x[i]=0;
        else{
            x[i]=1;
            c-=w[i];
        }
        x[N]=(f[1][C])?1:0;
    }

int main(){
    w[1]=100;
    w[2]=14;
    w[3]=10;
    p[1]=20;
    p[2]=18;
    p[3]=15;
    bag();
    printf("the max :%d\n",f[1][C]);
    traceback();
    int i;
    for(i=1;i<=N;i++)
        printf("%d ",x[i]);
    printf("\n");
    return 0;
}
    

时间复杂度：bag是：O（nc)。如果c很大，则时间要比递归的长。

问题：背包容量c，从n个物品中选取装入背包，每个物品i的重量为wi，价值pi。在背包中物品不超过c的条件下，求装入背包中的。

分析：采用动态规划算法，假设f(i , y)：表示背包剩余容量为y，剩余物品为i，i+1，。。。，n。则状态转移方程为：

f(i , y)=max{f(i+1 ,y) , f(i+1 ,y-wi)+pi}  if y>=wi;  

f(i , y)=f(i+1 , y) if y<wi;

代码如下：

#include<stdio.h>

#define N 3
int w[N+1];
int p[N+1];

int max(int x ,int y){
    return (x>y)?x:y;
}

int maxf(int i,int y){
   if(i==N)
        return (y>=w[N])?p[N]:0;
   if(y<w[i])
       return maxf(i+1,y);
   else
       return max(maxf(i+1,y),maxf(i+1,y-w[i])+p[i]);
}

int main(){
    int c;

    c=116;
    w[1]=100;
    w[2]=14;
    w[3]=10;
    p[1]=20;
    p[2]=18;
    p[3]=15;
    printf("the max :%d\n",maxf(1,c));

    return 0;
}

时间复杂度：O（)。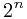 

由于使用了递归，空间复杂度也很大。

#include<stdio.h>

int maxsubarr(int a[],int n){
    int i,cur,max;
    
    cur=0;
    max=0;
    for(i=0;i<n;i++){
        cur+=a[i];
        if(cur>max)
            max=cur;
        if(cur<0)
            cur=0;
    }
    return max;
}

int main(){
    int a[]={-1,0,-2,1,2,3,4,-2,3,4,-1,2,4};
    int n=sizeof a/sizeof a[0];
    printf("the maxsum of the sub:%d\n",maxsubarr(a,n));

    return 0;
}

DFA可以用状态表来形象的表示，如下：

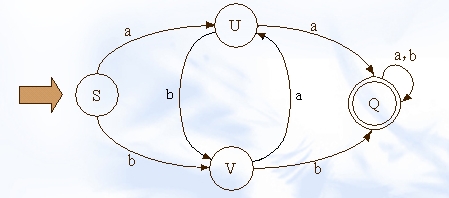
（图摘自http://www.javaeye.com/topic/336577，文章讲述了如何利用dfa来进行文字过滤）

它有点和边构成，其中点成为状态；边称为转移。状态中两种状态较为特殊：初始状态(s)和接受状态（Q）。

DFA精确定义：

DFA是一个 （Q,Σ ,§, q0,F) 构成的五元组，其中：

1.Q是有限状态集合。2.Σ 是有限字符集合。3.§是（Q,Σ )—>Q的转移函数。4。q0是初始状态。5.F是接受状态集合。

注：能被确定有限状态自动机识别的语言是正则语言。

DFA运算的精确定义：

设M= （Q,Σ ,§, q0,F)是一个DFA，w=w1w2w3...wn是一个language.那么，如果存在状态序列r0r1r2...rn，且满足以下三个条件：

（1）r0=q0;(2)§(ri , wi )=r(i+1) ,i=0,1,2,3,...,n (3) rn=F。

则称M接受w。

如何设计自动机：

设计自动机应该是极富创造力的工作，但是还是应该掌握一些构造的技巧：

(1)当你读字符串时，搞清楚应该记住关于字符串的什么信息。提取一些关键信息，确定可能性，得出状态集Q。

(2)通过转移来得到状态序列。

(3)确定初始、接受状态。

当然，以上只是简单的描述。

如何来描述DFA呢？

使用什么样的数据结构来描述DFA呢？

（1）根据状态图，当然可以使用矩阵来表示。

（2）也可以用Trie树来表示。可以，使用DAT。