算法 - webdancer's Blog

递归

对于递归算法，基本没有什么理解，但是有时候递归的用处还是很多的。记录几个例子。

1.用递归的方法，写函数itoa(n,s)，将整数转为字符串。

int i;
 
void itoa(int n,char s[]){
 
    if(n/10)
        itoa(n/10,s);
    else{
        i=0;
        if(n<0)
            s[i++]='-';
    }
    s[i++]=n%10+'0';
    s[i]='\0';
}

2.用递归方法，写函数reverse1(s)，将字符串倒置。

void swap(char *i,char *j){
    char tmp;
 
    tmp=*i;
    *i=*j;
    *j=tmp;
}
void reverse0(char s[],int i,int n){
    int j;
 
    j=n-(i+1);
    if(i<j){
        swap(&s[i],&s[j]);
        reverse0(s,++i,n);
    }
}
void reverse1(char s[]){
     
    reverse0(s,0,strlen(s));
 
}

3.Fibonacci数列的递归实现。

int fibonacci(int n){
    if(n<2)
        return n;
    else
        return fibonacci(n-1)+fibonacci(n-2);
}

4.求最大公约数。

int gcd(int x,int y){
   if(y==0)
       return x;
   else
       return gcd(y,x%y);
}

递归：函数不断调用自身，直到遇到结束条件停止。

代码简洁，容易理解。但是，递归过程会消耗大量的栈空间，不适合嵌入式系统或者内核态编程。

shell排序算法

shell排序算法是一种插入排序算法，直接的插入算法很简单，shell算法不同于直接插入的插入时小步挪动，而做长距离的跳动。它由Donald Shell于1959年提出。

shell算法也叫作“减少增量的排序算法”，每一遍通过增量h,使得那些相距h的记录排序。增量的序列不是固定的，确定最好的增量序列需要大量的数学知识。

shell算法：

<1>确定增量序列S[ t]。

<2>对给出的记录，按照增量序列S，进行t遍排序。

<3>对每遍进行直接插入。

/*为了编程方便，增量序列采用：
[n/2,n/4,......,1].实际的增量序列很是有趣。
*/
void shsort(int a[],int n){
    int i,j;
    for(i=n/2;i>=1;i/=2){
        for(j=i;j<n;j++){
            int k;
            for(k=j-i;k>=0&&a[k]>a[k+i];k-=i){
                int t=a[k];
                a[k]=a[k+i];
                a[k+i]=t;
            }
        }
    }
}   

我觉得还是挺有趣的，注意算法在利用直接插入时的方法，后面的元素不断的插入。

排序算法

我的算法可以说应该是很烂，归结起来：(1)不善总结，无法融汇贯通，与性格有关。(2)经常忘记，无法应用的好，与智商有关。我觉得：智商不高，还可以在计算机世界里混，但是若是性格不好，不能坚持，我觉得难有成绩。现在，该录正题了。

排序到底有什么用呢？对于我来说，我以前没有认真思考过这个问题，在Tao里，作者总结了一下,这里记录一下：

(1)解决“一起性”问题，把具有相同标志的项目连在一起。其实，sort在英文中就有分类的意思。把相同的东西归到一起，排序实在是好呀！

(2)匹配在两个文件或更多的文件中的项。排好序就可以顺序的扫描，而不用跳来跳去。

(3)通过键码查询信息。很多的检索算法用得到排序，向我们熟悉的二分查找，不就是对已经排好序的序列。

排序分为：内部排序和外部排序。所有的数据都可以放入主存中时，采用内部排序；当不能完全的放入主区，则只能采用外部排序。我还是先学习一下内部排序。

(1)直接插入排序。这种排序思想简单，就是在已经排好序的序列中，插入元素。

/*直接插入*/
void chsort(int a[],int n){
    int j,k;
    for(j=1;j<n;j++){
        k=a[j];
        int i=j-1;
        while(a[i]>k){
            a[i+1]=a[i];
            i--;
        }
        a[i+1]=k;
    }
}

(2)通过交换排序。

冒泡排序：

/*冒泡排序*/
void bsort(int a[],int n){
     int isch=1 , i,j;
     for(i=n-1;i>0&&isch;i--){
         isch=0;
         for(j=0;j<=i;j++){
             if(a[j]>a[j+1]){
                 int t;
                 t=a[j];
                 a[j]=a[j+1];
                 a[j+1]=t;
                 isch=1;
             }
         }
     }
}

快速排序：

/*快速排序的划分方式,a[r] 有最大的值。*/
void sortone(int a[],int l,int r){
    if(l>=r) return;
    int i=l+1,j=r;
    int base=a[l];
    while(i<j){
    while(a[i]<base)
        i++;
    while(a[j]>base)
        j--;
    if(i<j){
    int t=a[i];
    a[i]=a[j];
    a[j]=t;
    }
    }
    a[l]=a[j];
    a[j]=base;
    /*递归的调用sortone*/
    sortone(a,l,j-1);//  First, the wrong is: sortone(a,l,j).
    sortone(a,j+1,r);
}
/*为了排序的接口统一*/
void qusort(int a[],int n){
    sortone(a,0,n-1);
}

快速排序分析：

//使用快排对a[0...n-1]进行排序。

从a[0...n-1]中选择支点，把剩下的分为两段：left ，right；左边的都小于支点，右边的都大于支点。然后，递归的来对left，right进行排序，最后的结果为：left ,支点，right。

如何选择支点进行划分left,right会严重的影响快排的效率，我选择了教科书上的给出支点a[0]。但是，不是很好呀！快排对已经有序的序列进行排序，时间复杂度会上升的O(n2)，偏爱无序的序列。

不知道C函数库中的:

1	`void` `qsort(` `void` `buf,` `size_t` `num,` `size_t` `size,` `int` `(compare)(const` `void` `,` `const` `void` `) );`

如何实现的。

(3)选择排序。

/*直接选择排序*/
void xzsort(int a[],int n){
    int j;
    for(j=n-1;j>0;j--){
        int maxIndex=0,i;
        for(i=1;i<=j;i++)
            if(a[i]>a[maxIndex])
                maxIndex=i;
        int t;
        t=a[maxIndex];
        a[maxIndex]=a[j];
        a[j]=t;
    }
}

利用MAXHEAP来实现选择排序应该是一种很好的方法。MaxHeap数据结构的构建还是比较复杂的，涉及到构建堆，插入，删除MAX等。感觉在构建复杂的数据类型时，c++/java等引入了类的语言还是简单呀！

有限自动机（DFA)分析

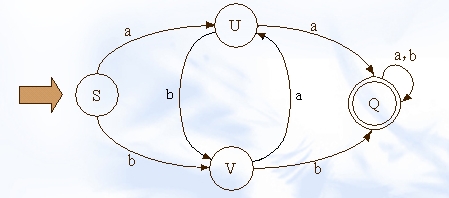
DFA可以用状态表来形象的表示，如下：

（图摘自http://www.javaeye.com/topic/336577，文章讲述了如何利用dfa来进行文字过滤）

它有点和边构成，其中点成为状态；边称为转移。状态中两种状态较为特殊：初始状态(s)和接受状态（Q）。

DFA精确定义：

DFA是一个（Q,Σ ,§, q0,F) 构成的五元组，其中：

1.Q是有限状态集合。2.Σ 是有限字符集合。3.§是（Q,Σ )—>Q的转移函数。4。q0是初始状态。5.F是接受状态集合。

注：能被确定有限状态自动机识别的语言是正则语言。

DFA运算的精确定义：

设M= （Q,Σ ,§, q0,F)是一个DFA，w=w1w2w3...wn是一个language.那么，如果存在状态序列r0r1r2...rn，且满足以下三个条件：

（1）r0=q0;(2)§(ri , wi )=r(i+1) ,i=0,1,2,3,...,n (3) rn=F。

则称M接受w。

如何设计自动机：

设计自动机应该是极富创造力的工作，但是还是应该掌握一些构造的技巧：

(1)当你读字符串时，搞清楚应该记住关于字符串的什么信息。提取一些关键信息，确定可能性，得出状态集Q。

(2)通过转移来得到状态序列。

(3)确定初始、接受状态。

当然，以上只是简单的描述。

如何来描述DFA呢？

使用什么样的数据结构来描述DFA呢？

（1）根据状态图，当然可以使用矩阵来表示。

（2）也可以用Trie树来表示。可以，使用DAT。

大数乘法，加法，除法运算 (转)

大数乘法，加法，除法

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

/*  写写大整数的一些算法,网上也可以找到，不过没有完整的
*   程序，于是写写比较完整的程序，发在Blog上
*/
#include <stdio.h>
#define MAXINT 1000
int compare(int a[],int b[]);
int bigplus(int a[],int b[],int c[]);
int bigsub(int a[],int b[],int c[]);
int bigmult(int a[],unsigned int b,int c[]);
int bigmult2(int a[],int b[],int c[]);
int bigdiv(int a[],unsigned int b,int c[],int *d); 
int bigdiv2(int a[],int b[],int c[],int d[]);
int main(int argc, char *argv[])
{
  int a[MAXINT]={10,5,4,6,5,4,3,2,1,1,1};     //被乘数或被除数 
  int b[MAXINT]={7,7,6,5,4,3,2,1};             //乘数或除数 
  int c[MAXINT],d[MAXINT];                    //c[]存放商，d[]存放余数 
  int div=1234;                               //小乘数或小除数 
  int k=0;
  int *res=&k;                                //小余数整数指针 
  bigplus(a,b,c); 
  bigsub(a,b,c); 
  bigmult(a,div,c); 
  bigmult2(a,b,c);
  bigdiv(a,div,c,res);
  bigdiv2(a,b,c,d);
  getchar();
  return 0;
}
int compare(int a[],int b[])          //比较大整数的大小 
{
    int i;
    if (a[0]>b[0]) return 1;          //比较a,b的位数确定返回值 
    else if (a[0]<b[0]) return -1;
    else                              //位数相等时的比较 
    {
        i=a[0];
        while (a[i]==b[i])            //逐位比较 
           i--;
        if (i==0) return 0;
        else if (a[i]>b[i]) return 1;
        else return -1;
    }
}
int bigplus(int a[],int b[],int c[])  //大整数加法 
{
    int i,len;
    len=(a[0]>b[0]?a[0]:b[0]);  //a[0] b[0]保存数组长度，len为较长的一个 
    for(i=0;i<MAXINT;i++)       //将数组清0 
        c[i]=0;
    for (i=1;i<=len;i++)        //计算每一位的值 
    {
        c[i]+=(a[i]+b[i]);
        if (c[i]>=10)
        {
           c[i]-=10;            //大于10的取个位 
           c[i+1]++;            //高位加1 
        }
    }
    if (c[i+1]>0) len++;
        c[0]=len;                //c[0]保存结果数组实际长度 
    printf("Big integers add: "; 
    for (i=len;i>=1;i--)
                printf("%d",c[i]); //打印结果 
        printf("\n";
    return 0;
}
int bigsub(int a[],int b[],int c[]) //大整数减法 
{
    int i,len;
    len=(a[0]>b[0]?a[0]:b[0]);  //a[0]保存数字长度，len为较长的一个 
    for(i=0;i<MAXINT;i++)       //将数组清0 
        c[i]=0;
    if (compare(a,b)==0)        //比较a,b大小 
    {
       printf("Result:0";
       return 0; 
    }
    else if (compare(a,b)>0)
    for (i=1;i<=len;i++)        //计算每一位的值 
    {
        c[i]+=(a[i]-b[i]); 
        if (c[i]<0)
        {
           c[i]+=10;            //小于0的原位加10 
           c[i+1]--;            //高位减1 
        }
    }
    else
        for (i=1;i<=len;i++)        //计算每一位的值 
        {
        c[i]+=(b[i]-a[i]); 
        if (c[i]<0)
        {
           c[i]+=10;            //小于0原位加10 
           c[i+1]--;            //高位减1 
        }
        }
    while (len>1 && c[len]==0)  //去掉高位的0 
        len--;
    c[0]=len;
    printf("Big integers sub= ";
    if (a[0]<b[0]) printf("-";
    for(i=len;i>=1;i--)         //打印结果 
        printf("%d",c[i]);
    printf("\n";
    return 0;
}
int bigmult(int a[],unsigned int b,int c[])//高精度乘以低精度 
{
    int len,i;
    for (i=0;i<MAXINT;i++)                  //数组清0 
      c[i]=0;
    len=a[0];
    for(i=1;i<=len;i++)                     //对每一位计算 
    {
       c[i]+=a[i]*b;
       c[i+1]+=c[i]/10;
       c[i]%=10;
    }
    while (c[++len]>=10)                    //处理高位 
    {
       c[len+1]=c[len]/10;
       c[len]%=10;
    }
    if (c[len]==0) len--;                   //处理高进位为0情况
    printf("Big integrs multi small integer: "; 
    for (i=len;i>=1;i--)
        printf("%d",c[i]);
    printf("\n"; 
}
int bigmult2(int a[],int b[],int c[])      //高精度乘以高精度 
{
    int i,j,len;
    for (i=0;i<MAXINT;i++)                  //数组清0 
        c[i]=0;
    for (i=1;i<=a[0];i++)                  //被乘数循环 
      for (j=1;j<=b[0];j++)                //乘数循环 
      {
         c[i+j-1]+=a[i]*b[j];              //将每一位计算累加 
         c[i+j]+=c[i+j-1]/10;              //将每一次结果累加到高一位 
         c[i+j-1]%=10;                     //计算每一次的个位 
      }
   len=a[0]+b[0];                          //取最大长度 
   while (len>1 && c[len]==0)              //去掉高位0 
      len--;
   c[0]=len;
   printf("Big integers multi: ";
   for (i=len;i>=1;i--)                    //打印结果 
      printf("%d",c[i]);
   printf("\n";  
}
int bigdiv(int a[],unsigned int b,int c[],int *d) //高精度除以低精度 
{                                           //a[] 为被乘数,b为除数,c[]为结果,d为余数 
    int i,len;                               
    len=a[0];                          //len为a[0]的数组长度  
    for (i=len;i>=1;i--)
    {
       (*d)=10*(*d)+a[i];                        //计算每一步余数 
       c[i]=(*d)/b;                           //计算每一步结果 
       (*d)=(*d)%b;                              //求模余数 
    } 
    while (len>1 && c[len]==0) len--;        //去高位0
    printf("Big integer div small integer: "; 
    for (i=len;i>=1;i--)                    //打印结果 
      printf("%d",c[i]);
    printf("\tArithmetic compliment:%d",*d); 
    printf("\n"; 
}
int bigdiv2(int a[],int b[],int c[],int d[])  //高精度除以高精度 
{
   int i,j,len;
   if (compare(a,b)<0)                        //被除数较小直接打印结果 
   {
     printf("Result:0";
     printf("Arithmetic compliment:";
     for (i=a[0];i>=1;i--) printf("%d",a[i]);
     printf("\n";
     return -1;            
   }
   for (i=0;i<MAXINT;i++)                     //商和余数清0 
   {
      c[i]=0;
      d[i]=0;
   }
   len=a[0];d[0]=0;
   for (i=len;i>=1;i--)                       //逐位相除 
   {
      for (j=d[0];j>=1;j--)
        d[j+1]=d[j];
      d[1]=a[i];                              //高位*10+各位 
      d[0]++;                                 //数组d长度增1 
      while (compare(d,b)>=0)                 //比较d,b大小 
      {
            for (j=1;j<=d[0];j++)              //做减法d-b 
            {
                d[j]-=b[j];
                if (d[j]<0)
                {
                   d[j]+=10;
                   d[j+1]--;
                }
            }
                while (j>0 && d[j]==0)        //去掉高位0 
                      j--;
                d[0]=j;
            c[i]++;                           //商所在位值加1 
      }
   }
   j=b[0];
   while (c[j]==0 && j>0) j--;                //求商数组c长度 
     c[0]=j;
   printf("Big integers div result: "; 
   for (i=c[0];i>=1;i--)                      //打印商 
     printf("%d",c[i]);
   printf("\tArithmetic compliment: ";       //打印余数 
   for (i=d[0];i>=1;i--)
     printf("%d",d[i]);
   printf("\n";
}

trie tree （转）

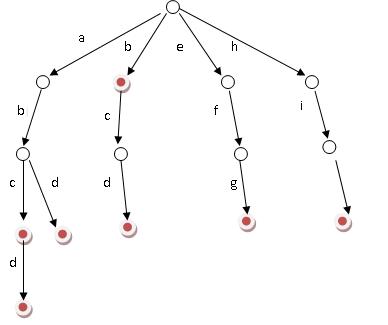
Trie,又称字典树、单词查找树,是一种树形结构，用于保存大量的字符串。它的优点是：利用字符串的公共前缀来节约存储空间。

相对来说,Trie树是一种比较简单的数据结构.理解起来比较简单,正所谓简单的东西也得付出代价.故Trie树也有它的缺点,Trie树的内存消耗非常大.当然,或许用左儿子右兄弟的方法建树的话,可能会好点.

其基本性质可以归纳为：
1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符都不相同。

其基本操作有:查找插入和删除,当然删除操作比较少见.我在这里只是实现了对整个树的删除操作,至于单个word的删除操作也很简单.

搜索字典项目的方法为：

(1) 从根结点开始一次搜索；

(2) 取得要查找关键词的第一个字母，并根据该字母选择对应的子树并转到该子树继续进行检索；

(3) 在相应的子树上，取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。

(4) 迭代过程……

(5) 在某个结点处，关键词的所有字母已被取出，则读取附在该结点上的信息，即完成查找。
其他操作类似处理.

    <span style="font-family: verdana,geneva,sans-serif;">  Name: Trie树的基本实现 
Author: MaiK 
Description: Trie树的基本实现 ,包括查找 插入和删除操作*/
#include<algorithm>
#include<iostream>
using namespace std;
 
const int sonnum=26,base='a';
struct Trie
{
    int num;//to remember how many word can reach here,that is to say,prefix
    bool terminal;//If terminal==true ,the current point has no following point
    struct Trie *son[sonnum];//the following point
};
Trie *NewTrie()// create a new node
{
    Trie *temp=new Trie;
    temp->num=1;temp->terminal=false;
    for(int i=0;i<sonnum;++i)temp->son[i]=NULL;
    return temp;
}
void Insert(Trie *pnt,char *s,int len)// insert a new word to Trie tree
{
    Trie *temp=pnt;
    for(int i=0;i<len;++i)
    {
        if(temp->son[s[i]-base]==NULL)temp->son[s[i]-base]=NewTrie();
        else temp->son[s[i]-base]->num++;
        temp=temp->son[s[i]-base];
    }
    temp->terminal=true;
}
void Delete(Trie *pnt)// delete the whole tree
{
    if(pnt!=NULL)
    {
        for(int i=0;i<sonnum;++i)if(pnt->son[i]!=NULL)Delete(pnt->son[i]);
        delete pnt; 
        pnt=NULL;
    }
}
Trie* Find(Trie *pnt,char *s,int len)//trie to find the current word
{
    Trie *temp=pnt;
    for(int i=0;i<len;++i)
        if(temp->son[s[i]-base]!=NULL)temp=temp->son[s[i]-base];
        else return NULL;
    return temp;
} 
</span>