算法 - webdancer's Blog
回溯法
回溯法:从问题的某一种状态(初始状态)出发,搜索从这种状态出发所能达到的所有“状态”,当一条路走到“尽头”的时候(不能再前进),再后退一步或若干步,从另一种可能“状态”出发,继续搜索,直到所有的“路径”(状态)都试探过。这种不断“前进”、不断“回溯”寻找解的方法,就称作“回溯法”。
回溯算法:
- 形式化解的结构,根据形式描述,建立解树。解树的每个非叶子节点描述一类可行解,而叶子节点通常描述一个可行解。
- 利用深度优先搜索解空间。算法根据目标函数,确定节点所代表解的优化程度,当访问叶子节点时,解就唯一的确定了;访问中间节点时还没法唯一的确定,无法计算目标函数值。利用启发函数和分支定界,避免移动到不可能产生解的子空间。问题的解空间通常是在搜索问题的解的过程中动态产生的,这是回溯算法的一个重要特性。
解空间:
回溯算法的解空间一般分为:子集树和排列树。
子集树:二叉树来表示,较为熟悉。
排列树:第一层树有n个选择,第二层有n-1个选择,以此类推,直到叶子节点。
子集树和排列树都是“隐式图”。
子集树遍历的伪代码:
void backtrack(int t)
{
if(t>n)
output(x);
else
for(int i=0; i<=1; i++)
{
x[t] = i;
backtrack(t+1);
}
}
排列树遍历的伪代码:
void backtrack(int t)
{
if(t>n)
output(x);
else
for(int i=t; i<=n; i++)
{
swap(x[t], x[i]);
backtrace(t+1);
swap(x[t], x[i]);
}
}
0/1背包的非递归动态规划算法
上次记录了,0/1背包问题动态规划的递归实现,下面记录一下也是动态规划的非递归实现。主要是对f函数结果的记录,使得不用像递归中的重复计算。
#include<stdio.h>
#include<stdlib.h>
#define max(a,b) (a)>(b)?(a):(b)
#define min(a,b) (a)<(b)?(a):(b)
#define N 3
#define C 116
int p[N+1];
int w[N+1];
int f[N+1][C+1];
int x[N+1];
void bag(){
int y,ymax,i;
ymax=min(w[N]-1,C);
for(y=0;y<ymax;y++)
f[N][y]=0;
for(y=w[N];y<C;y++)
f[N][y]=p[N];
for(i=N-1;i>1;i--){
ymax=min(w[i]-1,C);
for(y=0;y<ymax;y++)
f[i][y]=f[i+1][y];
for(y=w[N];y<C;y++)
f[i][y]=max(f[i+1][y],f[i+1][y-w[i]]+p[i]);
}
f[1][C]=f[2][C];
if(C>w[1])
f[1][C]=max(f[2][C],f[2][C-w[1]]+p[1]);
}
void traceback(){
int i,c;
c=C;
for(i=1;i<N;i++)
if(f[i][c]==f[i+1][c])
x[i]=0;
else{
x[i]=1;
c-=w[i];
}
x[N]=(f[1][C])?1:0;
}
int main(){
w[1]=100;
w[2]=14;
w[3]=10;
p[1]=20;
p[2]=18;
p[3]=15;
bag();
printf("the max :%d\n",f[1][C]);
traceback();
int i;
for(i=1;i<=N;i++)
printf("%d ",x[i]);
printf("\n");
return 0;
}
时间复杂度:bag是:O(nc)。如果c很大,则时间要比递归的长。
0/1背包问题
问题:背包容量c,从n个物品中选取装入背包,每个物品i的重量为wi,价值pi。在背包中物品不超过c的条件下,求装入背包中的。
分析:采用动态规划算法,假设f(i , y):表示背包剩余容量为y,剩余物品为i,i+1,。。。,n。则状态转移方程为:
f(i , y)=max{f(i+1 ,y) , f(i+1 ,y-wi)+pi} if y>=wi;
f(i , y)=f(i+1 , y) if y<wi;
代码如下:
#include<stdio.h>
#define N 3
int w[N+1];
int p[N+1];
int max(int x ,int y){
return (x>y)?x:y;
}
int maxf(int i,int y){
if(i==N)
return (y>=w[N])?p[N]:0;
if(y<w[i])
return maxf(i+1,y);
else
return max(maxf(i+1,y),maxf(i+1,y-w[i])+p[i]);
}
int main(){
int c;
c=116;
w[1]=100;
w[2]=14;
w[3]=10;
p[1]=20;
p[2]=18;
p[3]=15;
printf("the max :%d\n",maxf(1,c));
return 0;
}
时间复杂度:O(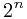 )。
)。
由于使用了递归,空间复杂度也很大。
子数组的最大和
#include<stdio.h>
int maxsubarr(int a[],int n){
int i,cur,max;
cur=0;
max=0;
for(i=0;i<n;i++){
cur+=a[i];
if(cur>max)
max=cur;
if(cur<0)
cur=0;
}
return max;
}
int main(){
int a[]={-1,0,-2,1,2,3,4,-2,3,4,-1,2,4};
int n=sizeof a/sizeof a[0];
printf("the maxsum of the sub:%d\n",maxsubarr(a,n));
return 0;
}
拓扑排序2
前一篇,学习了根据DFS,来进行拓扑排序的方法;今天看一下,按照贪婪算法来进行拓扑排序。主要的思想:找没有入度的顶点,放到队列里面;然后,逐渐从队列里删除顶点,加入一个数组,如果产生了新的没有入度的顶点,也加入队列,重复直到队列为空。
#include<stdio.h>
#include<stdlib.h>
#include"graph.c"
#include"queue.c"
#define MAX 100
int indeg[MAX];
int vl[MAX];
int *q;
void topolsort(Graph g){
int i,nv;
nv=g->nv;
for(i=0;i<nv;i++){
struct node * vnode;
vnode=g->adj[i];
while(vnode){
int u;
u=vnode->v;
indeg[u]++;
vnode=vnode->next;
}
}
q=initq(nv);
for(i=0;i<nv;i++)
if(indeg[i]==0)
add(q,i);
int iv;
iv=0;
while(!isempty()){
int u;
u=delete(q);
vl[iv++]=u;
struct node * unode;
unode=g->adj[u];
while(unode){
int v;
v=unode->v;
if(!(--indeg[v]))
add(q,v);
unode=unode->next;
}
}
}
int main(){
Graph g;
int n=6;
g=init(n);
edge e[8];
e[0].u=0;e[0].v=2;
e[1].u=0;e[1].v=3;
e[2].u=1;e[2].v=3;
e[3].u=1;e[3].v=4;
e[4].u=2;e[4].v=3;
e[5].u=2;e[5].v=5;
e[6].u=3;e[6].v=5;
e[7].u=4;e[6].v=5;
int i;
for(i=0;i<g->ne;i++)
insert(g,e[i]);
topolsort(g);
for(i=0;i<g->nv;i++)
printf("%d ",vl[i]);
printf("\n");
return 0;
}
时间复杂度分析:有向图的表示采用了邻接链表,所以时间复杂度为:Θ(V+E)。
拓扑排序
对一个DAG进行拓扑排序,结果为一个所有顶点构成的线性序列。序列满足:
对于<u,v>∈E(G),在序列中U出现在V的前面。
在算法导论中,给出的算法是:对DAG进行DFS遍历,计算每个顶点结束的时间,然后每完成一个顶点,将其加入到链表的头部。结果就是链表中的序列。
因此,对前面的DFS实现,稍加修改就可以了。此外,注意需要对原来的无向图实现修改。
代码:
#include<stdio.h>
#include"search.c"
extern int f[MAXV];
int * vq;
void reverse(int * a,int n){
int i,j;
for(i=1,j=n-1;i<j;i++,j--){
int t=a[i];
a[i]=a[j];
a[j]=t;
}
}
void dfsv1(Graph g,int u){
color[u]=GRAY;
time++;
d[u]=time;
struct node * vnode;
vnode=g->adj[u];
while(vnode){
int vv;
vv=vnode->v;
if(color[vv]==WHITE){
p[vv]=u;
dfsv1(g,vv);
}
vnode=vnode->next;
}
color[u]=BLACK;
time++;
f[u]=time;
add(vq,u);
//printf("%d ",u);
}
void topolsort(Graph g){
int i,v;
v=g->nv;
for(i=0;i<v;i++){
color[i]=WHITE;
p[i]=-1;
}
vq=initq(NUM);
time=0;
for(i=0;i<v;i++)
if(color[i]==WHITE){
dfsv1(g,i);
}
reverse(vq,v+1);
}
int main(){
Graph g;
int n=5;
g=init(n);
edge e[7];
e[0].u=0;e[0].v=1;
e[1].u=0;e[1].v=3;
e[2].u=1;e[2].v=2;
e[3].u=1;e[3].v=3;
e[4].u=1;e[4].v=4;
e[5].u=4;e[5].v=2;
e[6].u=3;e[6].v=4;
int i;
for(i=0;i<7;i++)
insert(g,e[i]);
topolsort(g);
for(i=1;i<=g->nv;i++)
printf("%d ",vq[i]);
printf("\n");
return 0;
}
找出数组中重复次数最多的元素并打印
题目:找
这道题其实在做汇编实验时,已经做过了。但是当时的思路还是太简单,现在又想了一下,可以先排序,然后遍历。这样如果采用快排,时间复杂度应为:O(nlogn+n)。代码:
总结:1.排序的应用,排序可以用来对相同的元素分类,使他们相邻,从而解决问题。
2.语言问题:在代码中注释掉的://printf("%d\n",(sizeof a )/(sizeof a[0])); Error。没有注意到:在函数中,a是个指针,而不是数组,分了错误,所以:在32位的机器上:(sizeof a )/(sizeof a[0])=1。
#include<stdio.h>
#include<stdlib.h>
int int_compare(const void * x1,const void * x2){
int * a=(int *)x1;
int * b=(int *)x2;
return (*a-*b);
}
void findremax(int a[],int n,int *m,int *c){
int index,count,maxc,i;
index=0;
count=1;
maxc=count;
//printf("%d\n",(sizeof a )/(sizeof a[0])); Error
for(i=1;i<n;i++){
if(a[i]==a[i-1])
count++;
else{
if(count>maxc){
maxc=count;
index=i-1;
}
count=1;
}
}
if(count>maxc){
maxc=count;
index=i-1;
}
*m=index;
*c=maxc;
}
int main(){
int maxindex,c;
int a[]={1,1,2,2,3,3,3,3,4,5,6,7,7,7,7,7,7};
int n=(sizeof a)/(sizeof a[0]);
maxindex=0;
c=0;
qsort(a,n,sizeof(a[0]),int_compare);
findremax(a,n,&maxindex,&c);
printf("%d appears %d times.\n",a[maxindex],c);
return 0;
}
图的搜索
最近学习图论,课程片中理论。但是,觉得还是实现一下好。就根据书上的写了图的BFS和DFS搜索算法。
1.图的实现,邻接链表。
#include<stdlib.h>
typedef struct {int u;int v;} edge;
struct node{int v;struct node * next;};
struct graph{int nv;int ne;struct node ** adj;};
typedef struct graph * Graph;
Graph init(int n){
Graph g=malloc(sizeof *g);// sizeof graph
g->nv=n;
g->ne=0;
g->adj=malloc((sizeof *(g->adj))*n);
int i;
for(i=0;i<g->nv;i++)
g->adj[i]=NULL;
return g;
}
void insert(Graph g,edge e){
int u,v;
u=e.u;
v=e.v;
struct node* unode=malloc(sizeof *unode);
unode->v=v;
unode->next=g->adj[u];
g->adj[u]=unode;
struct node* vnode=malloc(sizeof *vnode);
vnode->v=u;
vnode->next=g->adj[v];
g->adj[v]=vnode;
g->ne++;
}
2.队列实现。
#include<stdlib.h>
static int maxsize=0;
static int front=0;
static int rear=0;
int * queue;
int * initq(int max){
maxsize=max+1;
queue=malloc(sizeof(int)*maxsize);
front=rear=0;
return queue;
}
int add(int * q,int v){
if((rear+1)%maxsize==front)
return -1;
rear=(rear+1)%maxsize;
q[rear]=v;
return v;
}
int delete(int *q){
if(front==rear)
return -1;
front=(front+1)%maxsize;
return q[front];
}
int isempty(){
return (front==rear)?1:0;
}
3.搜索算法。
#include<stdlib.h>
#include<stdio.h>
#include"graph.c"
#include"queue.c"
/*bfs,dfs algos. from "introduction to algos".
*/
#define MAXV 1000
#define BIG (MAXV+1)
#define NUM 100
int color[MAXV];
int d[MAXV];
int p[MAXV];
int f[MAXV];
enum cl {WHITE,GRAY,BLACK};
int * q;
int time;
void bfs(Graph g,int s){
int i;
for(i=0;i<g->ne;i++){
color[i]=WHITE;
d[i]=-1;
p[i]=-1;
}
color[s]=GRAY;
d[s]=0;
p[s]=-1;
q=initq(NUM);
add(q,s);
while(!isempty()){
int u;
u=delete(q);
printf("%d u \n",u);
struct node * vnode=g->adj[u];
while(vnode){
int v;
v=vnode->v;
if(color[v]==WHITE){
color[v]=GRAY;
d[v]=d[u]+1;
p[v]=u;
add(q,v);
}
vnode=vnode->next;
}
color[u]=BLACK;
}
}
void dfsv(Graph g,int u){
color[u]=GRAY;
time++;
d[u]=time;
struct node * vnode;
vnode=g->adj[u];
while(vnode){
int vv;
vv=vnode->v;
if(color[vv]==WHITE){
p[vv]=u;
dfsv(g,vv);
}
vnode=vnode->next;
}
color[u]=BLACK;
time++;
f[u]=time;
}
void dfs(Graph g){
int i,v;
v=g->nv;
for(i=0;i<v;i++){
color[i]=WHITE;
p[i]=-1;
}
time=0;
for(i=0;i<v;i++){
if(color[i]==WHITE)
dfsv(g,i);
}
}
void printpath(Graph g,int s,int v){
if(v==s)
printf("%d ",s);
else if(p[v]==-1)
printf("no path from s to v\n");
else
{
printpath(g,s,p[v]);
printf("%d ",v);
}
}
int main(){
Graph g;
int n=5;
g=init(n);
edge e[7];
e[0].u=0;e[0].v=1;
e[1].u=0;e[1].v=3;
e[2].u=1;e[2].v=2;
e[3].u=1;e[3].v=3;
e[4].u=1;e[4].v=4;
e[5].u=2;e[5].v=4;
e[6].u=3;e[6].v=4;
int i;
for(i=0;i<7;i++)
insert(g,e[i]);
bfs(g,0);
printpath(g,0,4);
printf("\n");
dfs(g);
printpath(g,0,4);
printf("\n");
return 0;
}
CODE过程中,指针的出错还是有,一定要注意动态分配内存的问题,在这个地方很容易出错。还有就是指向指针的指针问题。对于C来说,指针部分得多练多想呀!不知道,谁有好的理解。