Neural Networks笔记1 - webdancer's Blog
Neural Networks笔记1
1.继续八卦NN的历史
人工神经网络的研究者,试图创造一个大脑和机器处理信息的统一模型,在这个模型中,信息按照同意的规则进行处理。正如Frank Rosenblatt所希望的:
"the fundamental laws of organization which are common to all information handling systems, machines and men included, may eventually be understood."
2.Perceptron model
Perceptron是一种线性模型,只能把那些线性可分的数据进行分类,是一种只有输入输出层,而没有中间层的简单神经网络,示意图如下(输入,输出层的节点数目都是可以根据具体的问题改变):
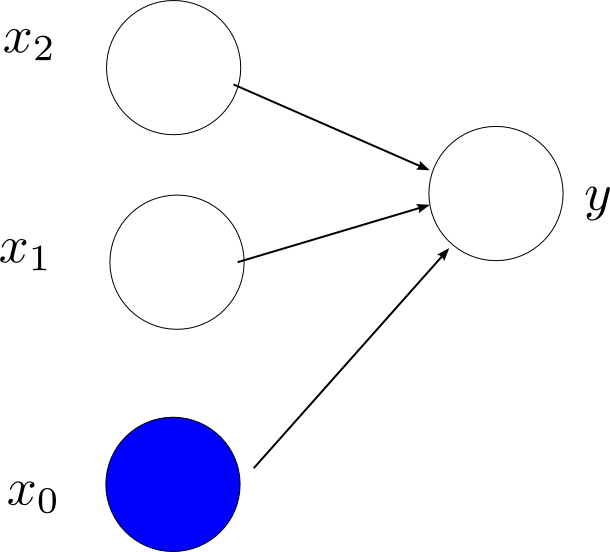
下面看一下Perceptron的模型,
其中,
模型训练
我们使用的一种称为perceptron criterion的误差函数,在这种误差函数中,对那些分类正确的训练实例其错误为0,对那些分类错误的实例,最小化−WTϕntn[1],所以误差函数的形式为:
其中,M为分类错误的实例集合。可以看出,Ep(W)是关于W的线性函数。有了目标函数,我们就可以使用sgd方法进行参数的训练。
Wt+1=Wt−η▽Ep(W)=Wt−η▽E(W)=Wt+ηϕntn
其中,t为训练的次数 ;η为学习系数,常用系数η=1。我们可以这样简单的理解上面的过程:在训练集合上,我们选择一个实例,用Perceptron function计算y(x),如果分类正确,则W值不变;如果分类错误,根据上面的讨论,更新W,如果我们把学习系数设为1,对于C1,我们在W上加上特征向量,对于C2,我们在W上减去特征向量。
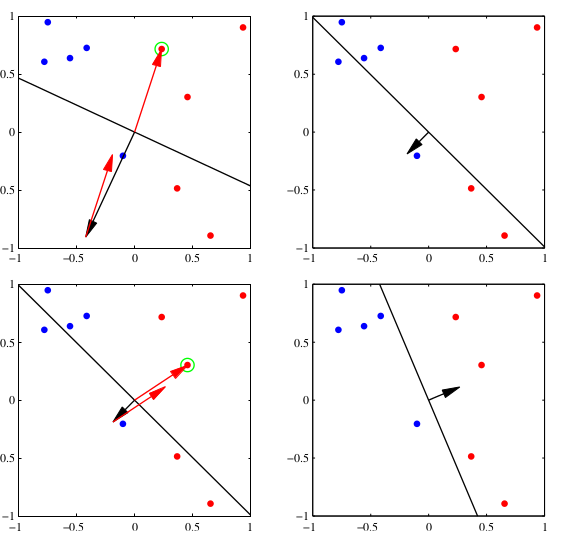
总结一下,算法如下:
过程如下图所示:
3.Perceptron模型的XOR问题
|
x1 |
x2 |
y |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
0 |
对于XOR问题,Perception无法解决,本质上是因为Perception是一种线性的分类器,无法处理像XOR这样的线性不可分问题,只能处理线性可分问题(这本质是由于基函数的数目是固定的)。下面具体看一下:
1.第一种情况,把y=0当作正类,y=1当作负类,则应满足:
上面的式子显然矛盾,所以Perception无法处理。
2.第二种情况,把y=1当作正类,y=0当作负类,则应满足:
{0<=0w1+w2<=0w1>0w2∗1>0
4.BP网络解决XOR问题
Bp网络相对于perceptron来说,引入了中间层(hidden layer),如果我们增加中间节点的数目,BP网络几乎可以模拟任何函数,这使得BP网络有了巨大的威力。下面看一下我们怎么用BP网络来解决XOR问题。
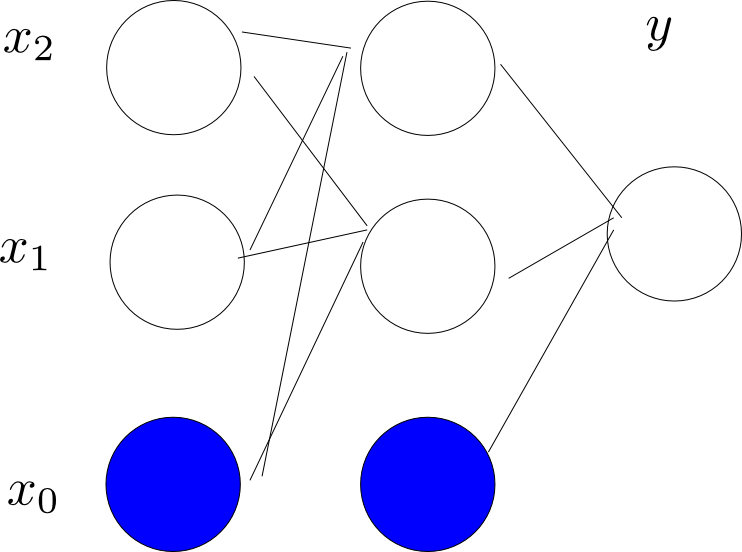
当然BP绝不限于解决像XOR这样的简单函数,它能够模拟很复杂的函数,例如:卷积神经网络(Convolutional neural network, CNN)在手写字符识别等问题中能取得非常好的效果,当然还有很多的新的NN网络的架构在不断的发现和研究。
2022年8月17日 21:21
Students taking the class 11 exams administered by the Uttarakhand Board may review the important model question paper from 2023 for better preparation. On the official website, you may obtain the 11th Important Model Question Paper for 2023 for the Science, Commerce, and Arts streams. However, the Board will shortly publish the condensed Important Model Question Paper 2023 for the upcoming academic year. Uttarakhand Intermediate Question Paper 2023 Students may verify the marking scheme and the Important Model Question Paper 2023 using this UK Board 11th Practice exam. The 11th Significant Model Question Paper from the Uttarakhand Board for 2023 also lists important themes for each subject, such as English, Economics, Geography, and Mathematics, unit by unit.